Automatic Solver Generator for Systems of Laurent Polynomial Equations

In computer vision applications, the following problem often arises: Given a family of (Laurent) polynomial systems with the same monomial structure but varying coefficients, find a solver that computes solutions for any family member as fast as possible. Under appropriate genericity assumptions, the dimension and degree of the respective polynomial ideal remain unchanged for each particular system in the same family. The state-of-the-art approach to solving such problems is based on elimination templates, which are the coefficient (Macaulay) matrices that encode the transformation from the initial polynomials to the polynomials needed to construct the action matrix. Knowing an action matrix, the solutions of the system are computed from its eigenvectors. The important property of an elimination template is that it applies to all polynomial systems in the family. In this paper, we propose a new practical algorithm that checks whether a given set of Laurent polynomials is sufficient to construct an elimination template. Based on this algorithm, we propose an automatic solver generator for systems of Laurent polynomial equations. The new generator is simple and fast; it applies to ideals with positive-dimensional components; it allows one to uncover partial $p$-fold symmetries automatically. We test our generator on various minimal problems, mostly in geometric computer vision. The speed of the generated solvers exceeds the state-of-the-art in most cases. In particular, we propose the solvers for the following problems: optimal 3-view triangulation, semi-generalized hybrid pose estimation and minimal time-of-arrival self-calibration. The experiments on synthetic scenes show that our solvers are numerically accurate and either comparable to or significantly faster than the state-of-the-art solvers.

Optimizing Elimination Templates by Greedy Parameter Search

We propose a new method for constructing elimination templates for efficient polynomial system solving of minimal problems in structure from motion, image matching, and camera tracking. We first construct a particular affine parameterization of the elimination templates for systems with a finite number of distinct solutions. Then, we use a heuristic greedy optimization strategy over the space of parameters to get a template with a small size. We test our method on 34 minimal problems in computer vision. For all of them, we found the templates either of the same or smaller size compared to the state-of-the-art. For some difficult examples, our templates are, e.g., 2.1, 2.5, 3.8, 6.6 times smaller. For the problem of refractive absolute pose estimation with unknown focal length, we have found a template that is 20 times smaller. Our experiments on synthetic data also show that the new solvers are fast and numerically accurate. We also present a fast and numerically accurate solver for the problem of relative pose estimation with unknown common focal length and radial distortion.

Relative Pose Estimation of Calibrated Cameras with Known $\mathrm{SE}(3)$ Invariants

The $\mathrm{SE}(3)$ invariants of a pose include its rotation angle and screw translation. In this paper, we present a complete comprehensive study of the relative pose estimation problem for a calibrated camera constrained by known $\mathrm{SE}(3)$ invariant, which involves 5 minimal problems in total. These problems reduces the minimal number of point pairs for relative pose estimation and improves the estimation efficiency and robustness. The $\mathrm{SE}(3)$ invariant constraints can come from extra sensor measurements or motion assumption. Different from conventional relative pose estimation with extra constraints, no extrinsic calibration is required to transform the constraints to the camera frame. This advantage comes from the invariance of $\mathrm{SE}(3)$ invariants cross different coordinate systems on a rigid body and makes the solvers more convenient and flexible in practical applications. Besides proposing the concept of relative pose estimation constrained by $\mathrm{SE}(3)$ invariants, we present a comprehensive study of existing polynomial formulations for relative pose estimation and discover their relationship. Different formulations are carefully chosen for each proposed problems to achieve best efficiency. Experiments on synthetic and real data shows performance improvement compared to conventional relative pose estimation methods.

Efficient Relative Pose Estimation for Cameras and Generalized Cameras in Case of Known Relative Rotation Angle

We propose two minimal solutions to the problem of relative pose estimation of (i) a calibrated camera from four points in two views and (ii) a calibrated generalized camera from five points in two views. In both cases, the relative rotation angle between the views is assumed to be known. In practice, such angle can be derived from the readings of a 3d gyroscope. We represent the rotation part of the motion in terms of unit quaternions in order to construct polynomial equations encoding the epipolar constraints. The Gr\"{o}bner basis technique is then used to efficiently derive the solutions. Our first solver for regular cameras significantly improves the existing state-of-the-art solution. The second solver for generalized cameras is novel. The presented minimal solvers can be used in a hypothesize-and-test architecture such as RANSAC for reliable pose estimation. Experiments on synthetic and real datasets confirm that our algorithms are numerically stable, fast and robust.

Self-Calibration of Cameras with Euclidean Image Plane in Case of Two Views and Known Relative Rotation Angle

The internal calibration of a pinhole camera is given by five parameters that are combined into an upper-triangular $3\times 3$ calibration matrix. If the skew parameter is zero and the aspect ratio is equal to one, then the camera is said to have Euclidean image plane. In this paper, we propose a non-iterative self-calibration algorithm for a camera with Euclidean image plane in case the remaining three internal parameters --- the focal length and the principal point coordinates --- are fixed but unknown. The algorithm requires a set of $N \geq 7$ point correspondences in two views and also the measured relative rotation angle between the views. We show that the problem generically has six solutions (including complex ones). The algorithm has been implemented and tested both on synthetic data and on publicly available real dataset. The experiments demonstrate that the method is correct, numerically stable and robust.

On Some Properties of Calibrated Trifocal Tensors

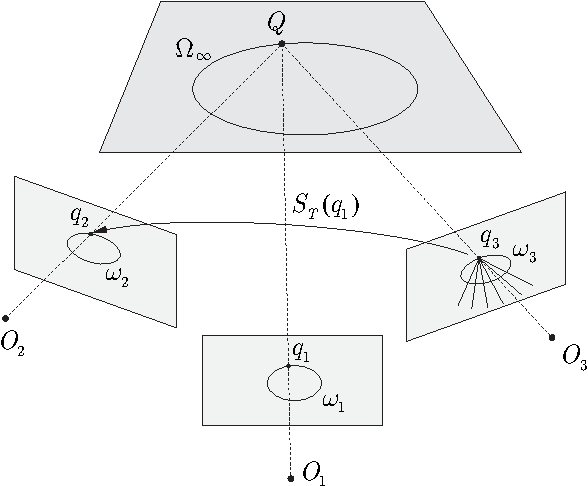
In two-view geometry, the essential matrix describes the relative position and orientation of two calibrated images. In three views, a similar role is assigned to the calibrated trifocal tensor. It is a particular case of the (uncalibrated) trifocal tensor and thus it inherits all its properties but, due to the smaller degrees of freedom, satisfies a number of additional algebraic constraints. Some of them are described in this paper. More specifically, we define a new notion --- the trifocal essential matrix. On the one hand, it is a generalization of the ordinary (bifocal) essential matrix, and, on the other hand, it is closely related to the calibrated trifocal tensor. We prove the two necessary and sufficient conditions that characterize the set of trifocal essential matrices. Based on these characterizations, we propose three necessary conditions on a calibrated trifocal tensor. They have a form of 15 quartic and 99 quintic polynomial equations. We show that in the practically significant real case the 15 quartic constraints are also sufficient.

A Minimal Six-Point Auto-Calibration Algorithm

A non-iterative auto-calibration algorithm is presented. It deals with a minimal set of six scene points in three views taken by a camera with fixed but unknown intrinsic parameters. Calibration is based on the image correspondences only. The algorithm is implemented and validated on synthetic image data.

An Algorithmic Solution to the Five-Point Pose Problem Based on the Cayley Representation of Rotations

We give a new algorithmic solution to the well-known five-point relative pose problem. Our approach does not deal with the famous cubic constraint on an essential matrix. Instead, we use the Cayley representation of rotations in order to obtain a polynomial system from epipolar constraints. Solving that system, we directly get relative rotation and translation parameters of the cameras in terms of roots of a 10th degree polynomial.

A Non-Iterative Solution to the Four-Point Three-Views Pose Problem in Case of Collinear Cameras

We give a non-iterative solution to a particular case of the four-point three-views pose problem when three camera centers are collinear. Using the well-known Cayley representation of orthogonal matrices, we derive from the epipolar constraints a system of three polynomial equations in three variables. The eliminant of that system is a multiple of a 36th degree univariate polynomial. The true (unique) solution to the problem can be expressed in terms of one of real roots of that polynomial. Experiments on synthetic data confirm that our method is robust enough even in case of planar configurations.