Snehal Bhayani
A Conic Transformation Approach for Solving the Perspective-Three-Point Problem
Apr 02, 2025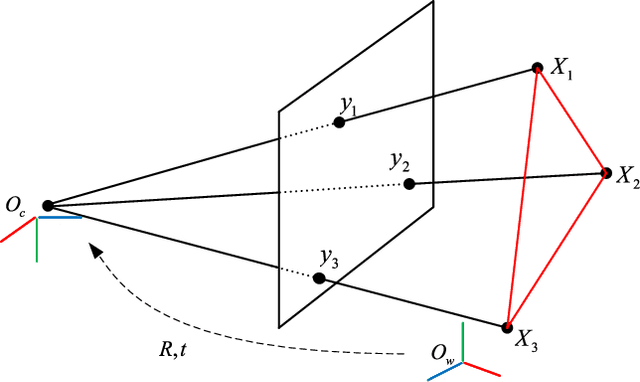
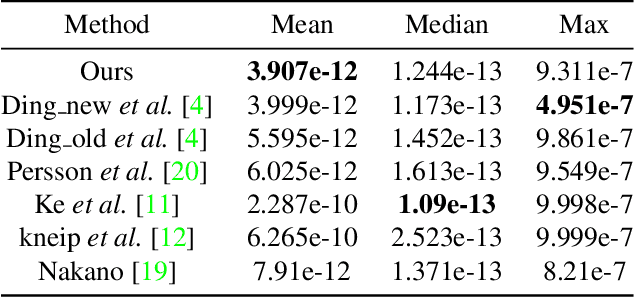
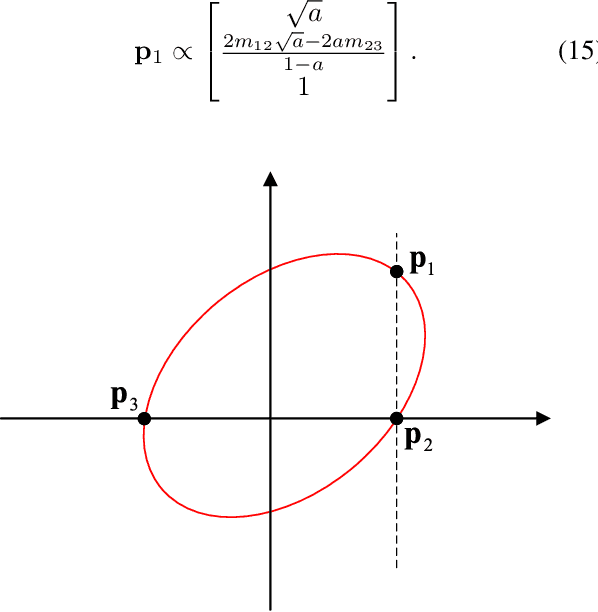
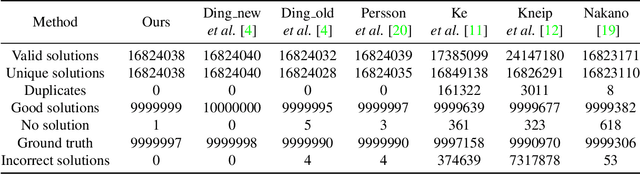
Abstract:We propose a conic transformation method to solve the Perspective-Three-Point (P3P) problem. In contrast to the current state-of-the-art solvers, which formulate the P3P problem by intersecting two conics and constructing a degenerate conic to find the intersection, our approach builds upon a new formulation based on a transformation that maps the two conics to a new coordinate system, where one of the conics becomes a standard parabola in a canonical form. This enables expressing one variable in terms of the other variable, and as a consequence, substantially simplifies the problem of finding the conic intersection. Moreover, the polynomial coefficients are fast to compute, and we only need to determine the real-valued intersection points, which avoids the requirement of using computationally expensive complex arithmetic. While the current state-of-the-art methods reduce the conic intersection problem to solving a univariate cubic equation, our approach, despite resulting in a quartic equation, is still faster thanks to this new simplified formulation. Extensive evaluations demonstrate that our method achieves higher speed while maintaining robustness and stability comparable to state-of-the-art methods.
Automatic Solver Generator for Systems of Laurent Polynomial Equations
Jul 01, 2023



Abstract:In computer vision applications, the following problem often arises: Given a family of (Laurent) polynomial systems with the same monomial structure but varying coefficients, find a solver that computes solutions for any family member as fast as possible. Under appropriate genericity assumptions, the dimension and degree of the respective polynomial ideal remain unchanged for each particular system in the same family. The state-of-the-art approach to solving such problems is based on elimination templates, which are the coefficient (Macaulay) matrices that encode the transformation from the initial polynomials to the polynomials needed to construct the action matrix. Knowing an action matrix, the solutions of the system are computed from its eigenvectors. The important property of an elimination template is that it applies to all polynomial systems in the family. In this paper, we propose a new practical algorithm that checks whether a given set of Laurent polynomials is sufficient to construct an elimination template. Based on this algorithm, we propose an automatic solver generator for systems of Laurent polynomial equations. The new generator is simple and fast; it applies to ideals with positive-dimensional components; it allows one to uncover partial $p$-fold symmetries automatically. We test our generator on various minimal problems, mostly in geometric computer vision. The speed of the generated solvers exceeds the state-of-the-art in most cases. In particular, we propose the solvers for the following problems: optimal 3-view triangulation, semi-generalized hybrid pose estimation and minimal time-of-arrival self-calibration. The experiments on synthetic scenes show that our solvers are numerically accurate and either comparable to or significantly faster than the state-of-the-art solvers.
Sparse resultant based minimal solvers in computer vision and their connection with the action matrix
Jan 16, 2023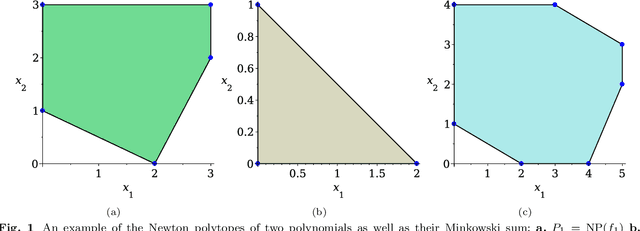
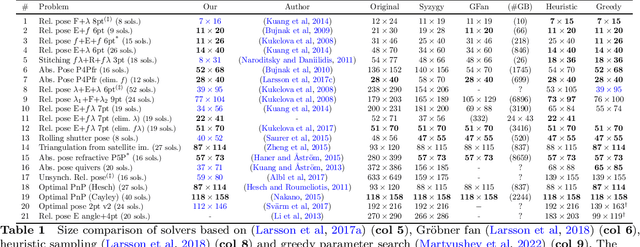
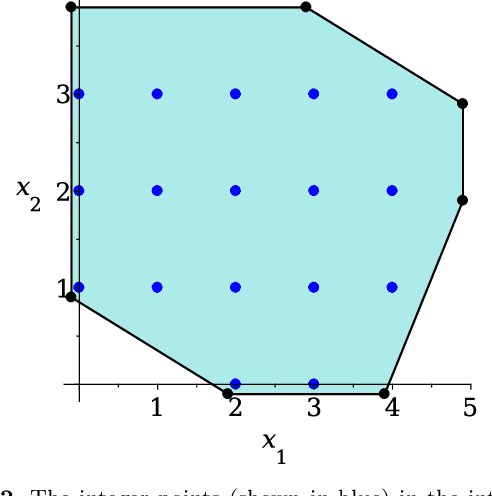
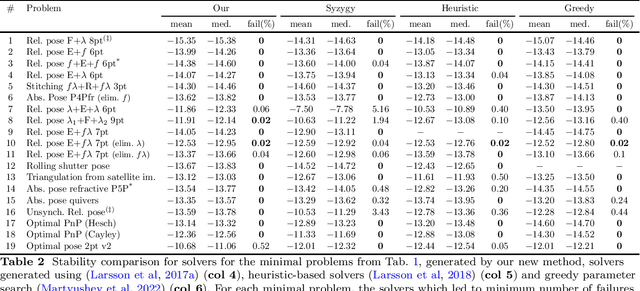
Abstract:Many computer vision applications require robust and efficient estimation of camera geometry from a minimal number of input data measurements, ie, solving minimal problems in a RANSAC framework. Minimal problems are usually formulated as complex systems of polynomial equations. Many state-of-the-art efficient polynomial solvers are based on the action matrix method that has been automated and highly optimised in recent years. In this paper we explore the theory of sparse resultants for generating minimal solvers and propose a novel approach based on a using an extra polynomial with a special form. We show that for some camera geometry problems our extra polynomial-based method leads to smaller and more stable solvers than the state-of-the-art Gr\"obner basis-based solvers. The proposed method can be fully automated and incorporated into existing tools for automatic generation of efficient polynomial solvers. It provides a competitive alternative to popular Gr\"obner basis-based methods for minimal problems in computer vision. Additionally, we study the conditions under which the minimal solvers generated by the state-of-the-art action matrix-based methods and the proposed extra polynomial resultant-based method, are equivalent. Specifically we consider a step-by-step comparison between the approaches based on the action matrix and the sparse resultant, followed by a set of substitutions, which would lead to equivalent minimal solvers.
Partially calibrated semi-generalized pose from hybrid point correspondences
Sep 29, 2022
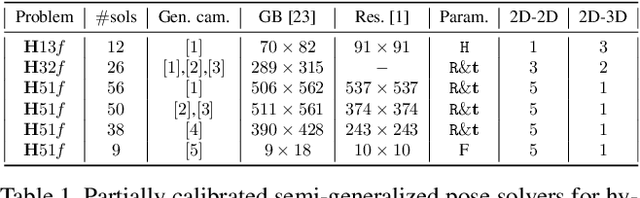
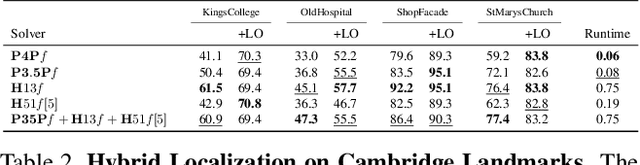
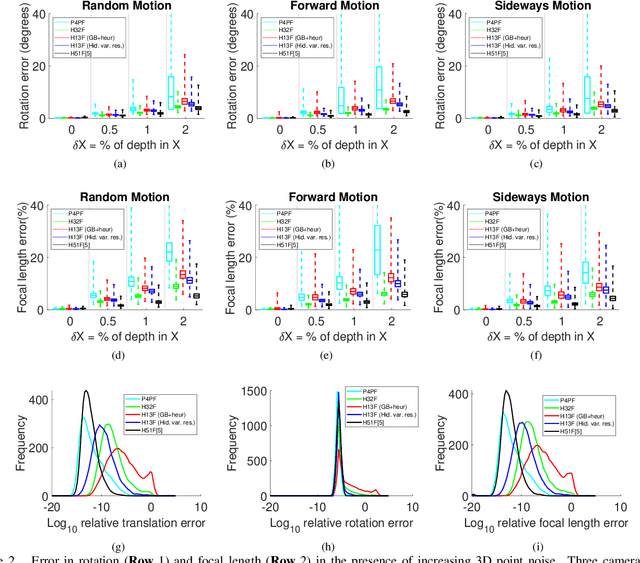
Abstract:In this paper we study the problem of estimating the semi-generalized pose of a partially calibrated camera, i.e., the pose of a perspective camera with unknown focal length w.r.t. a generalized camera, from a hybrid set of 2D-2D and 2D-3D point correspondences. We study all possible camera configurations within the generalized camera system. To derive practical solvers to previously unsolved challenging configurations, we test different parameterizations as well as different solving strategies based on the state-of-the-art methods for generating efficient polynomial solvers. We evaluate the three most promising solvers, i.e., the H51f solver with five 2D-2D correspondences and one 2D-3D correspondence viewed by the same camera inside generalized camera, the H32f solver with three 2D-2D and two 2D-3D correspondences, and the H13f solver with one 2D-2D and three 2D-3D correspondences, on synthetic and real data. We show that in the presence of noise in the 3D points these solvers provide better estimates than the corresponding absolute pose solvers.
Calibrated and Partially Calibrated Semi-Generalized Homographies
Mar 17, 2021



Abstract:In this paper, we propose the first minimal solutions for estimating the semi-generalized homography given a perspective and a generalized camera. The proposed solvers use five 2D-2D image point correspondences induced by a scene plane. One of them assumes the perspective camera to be fully calibrated, while the other solver estimates the unknown focal length together with the absolute pose parameters. This setup is particularly important in structure-from-motion and image-based localization pipelines, where a new camera is localized in each step with respect to a set of known cameras and 2D-3D correspondences might not be available. As a consequence of a clever parametrization and the elimination ideal method, our approach only needs to solve a univariate polynomial of degree five or three. The proposed solvers are stable and efficient as demonstrated by a number of synthetic and real-world experiments.
Computing stable resultant-based minimal solvers by hiding a variable
Jul 17, 2020


Abstract:Many computer vision applications require robust and efficient estimation of camera geometry. The robust estimation is usually based on solving camera geometry problems from a minimal number of input data measurements, i.e., solving minimal problems, in a RANSAC-style framework. Minimal problems often result in complex systems of polynomial equations. The existing state-of-the-art methods for solving such systems are either based on Gr\"obner bases and the action matrix method, which have been extensively studied and optimized in the recent years or recently proposed approach based on a sparse resultant computation using an extra variable. In this paper, we study an interesting alternative sparse resultant-based method for solving sparse systems of polynomial equations by hiding one variable. This approach results in a larger eigenvalue problem than the action matrix and extra variable sparse resultant-based methods; however, it does not need to compute an inverse or elimination of large matrices that may be numerically unstable. The proposed approach includes several improvements to the standard sparse resultant algorithms, which significantly improves the efficiency and stability of the hidden variable resultant-based solvers as we demonstrate on several interesting computer vision problems. We show that for the studied problems, our sparse resultant based approach leads to more stable solvers than the state-of-the-art Gr\"obner bases-based solvers as well as existing sparse resultant-based solvers, especially in close to critical configurations. Our new method can be fully automated and incorporated into existing tools for the automatic generation of efficient minimal solvers.
A sparse resultant based method for efficient minimal solvers
Dec 21, 2019



Abstract:Many computer vision applications require robust and efficient estimation of camera geometry. The robust estimation is usually based on solving camera geometry problems from a minimal number of input data measurements, i.e. solving minimal problems in a RANSAC framework. Minimal problems often result in complex systems of polynomial equations. Many state-of-the-art efficient polynomial solvers to these problems are based on Gr\"obner bases and the action-matrix method that has been automatized and highly optimized in recent years. In this paper we study an alternative algebraic method for solving systems of polynomial equations, i.e., the sparse resultant-based method and propose a novel approach to convert the resultant constraint to an eigenvalue problem. This technique can significantly improve the efficiency and stability of existing resultant-based solvers. We applied our new resultant-based method to a large variety of computer vision problems and show that for most of the considered problems, the new method leads to solvers that are the same size as the the best available Gr\"obner basis solvers and of similar accuracy. For some problems the new sparse-resultant based method leads to even smaller and more stable solvers than the state-of-the-art Gr\"obner basis solvers. Our new method can be fully automatized and incorporated into existing tools for automatic generation of efficient polynomial solvers and as such it represents a competitive alternative to popular Gr\"obner basis methods for minimal problems in computer vision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge