Sparse resultant based minimal solvers in computer vision and their connection with the action matrix

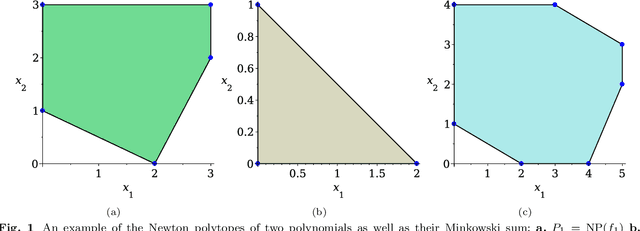
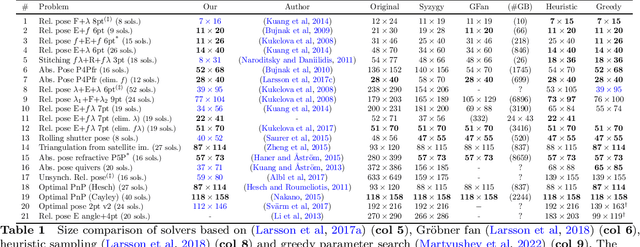
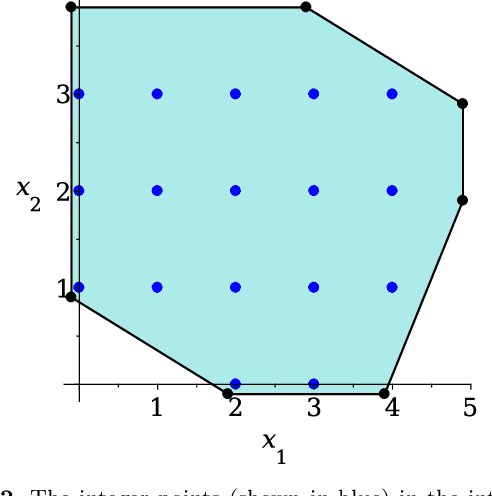
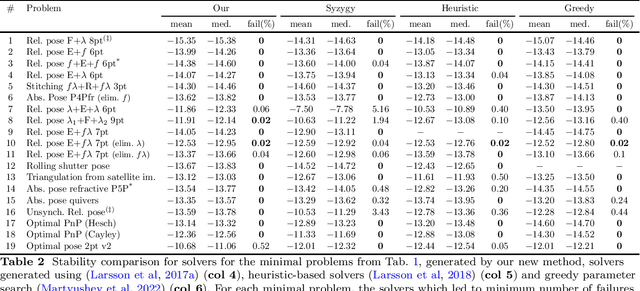
Many computer vision applications require robust and efficient estimation of camera geometry from a minimal number of input data measurements, ie, solving minimal problems in a RANSAC framework. Minimal problems are usually formulated as complex systems of polynomial equations. Many state-of-the-art efficient polynomial solvers are based on the action matrix method that has been automated and highly optimised in recent years. In this paper we explore the theory of sparse resultants for generating minimal solvers and propose a novel approach based on a using an extra polynomial with a special form. We show that for some camera geometry problems our extra polynomial-based method leads to smaller and more stable solvers than the state-of-the-art Gr\"obner basis-based solvers. The proposed method can be fully automated and incorporated into existing tools for automatic generation of efficient polynomial solvers. It provides a competitive alternative to popular Gr\"obner basis-based methods for minimal problems in computer vision. Additionally, we study the conditions under which the minimal solvers generated by the state-of-the-art action matrix-based methods and the proposed extra polynomial resultant-based method, are equivalent. Specifically we consider a step-by-step comparison between the approaches based on the action matrix and the sparse resultant, followed by a set of substitutions, which would lead to equivalent minimal solvers.