An Atlas for the Pinhole Camera

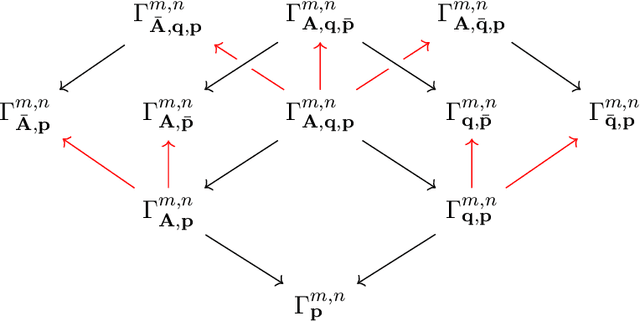
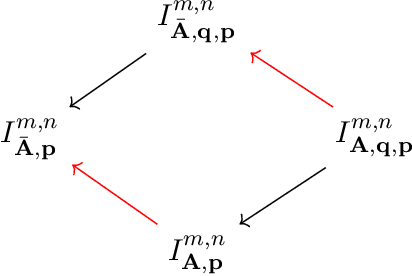
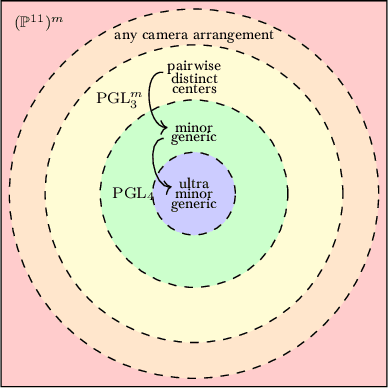
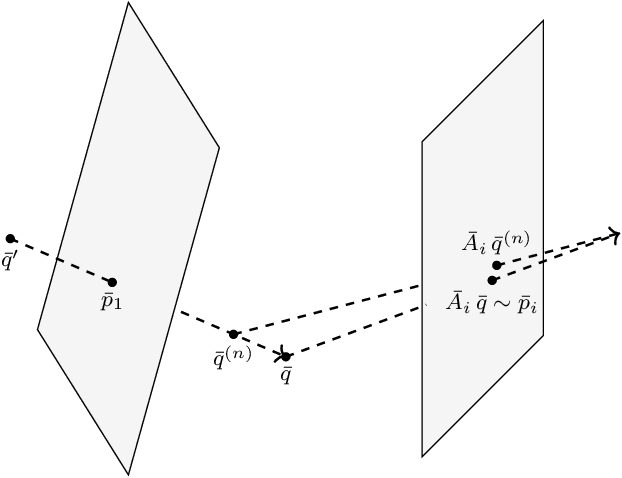
We introduce an atlas of algebro-geometric objects associated with image formation in pinhole cameras. The nodes of the atlas are algebraic varieties or their vanishing ideals related to each other by projection or elimination and restriction or specialization respectively. This atlas offers a unifying framework for the study of problems in 3D computer vision. We initiate the study of the atlas by completely characterizing a part of the atlas stemming from the triangulation problem. We conclude with several open problems and generalizations of the atlas.

Two Hilbert schemes in computer vision

We study multiview moduli problems that arise in computer vision. We show that these moduli spaces are always smooth and irreducible, in both the calibrated and uncalibrated cases, for any number of views. We also show that these moduli spaces always embed in suitable Hilbert schemes, and that these embeddings are open immersions for more than four views, extending and refining work of Aholt-Sturmfels-Thomas. In follow-up work, we will use the techniques developed here to give a new description of the essential variety that simultaneously recovers seminal work of Demazure and recent results of Kileel-Fl{\o}ystad-Ottaviani.