An Atlas for the Pinhole Camera

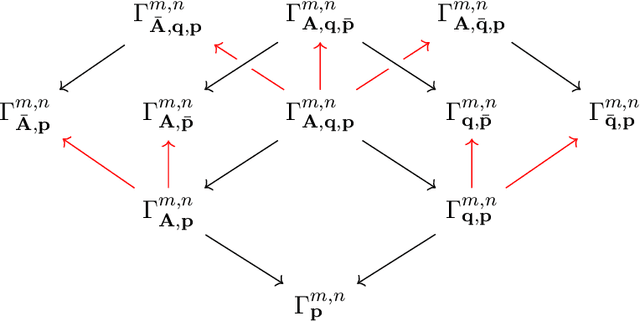
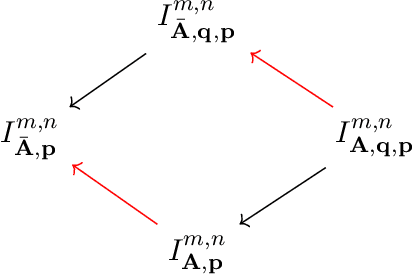
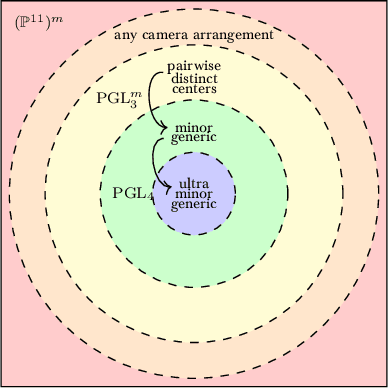
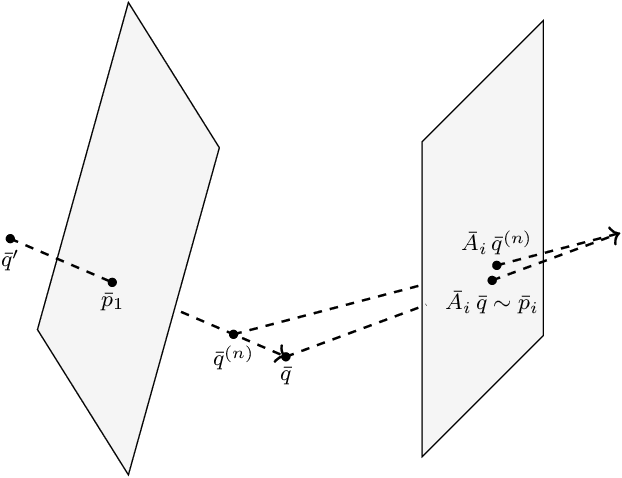
We introduce an atlas of algebro-geometric objects associated with image formation in pinhole cameras. The nodes of the atlas are algebraic varieties or their vanishing ideals related to each other by projection or elimination and restriction or specialization respectively. This atlas offers a unifying framework for the study of problems in 3D computer vision. We initiate the study of the atlas by completely characterizing a part of the atlas stemming from the triangulation problem. We conclude with several open problems and generalizations of the atlas.

A Hilbert Scheme in Computer Vision

Multiview geometry is the study of two-dimensional images of three-dimensional scenes, a foundational subject in computer vision. We determine a universal Groebner basis for the multiview ideal of n generic cameras. As the cameras move, the multiview varieties vary in a family of dimension 11n-15. This family is the distinguished component of a multigraded Hilbert scheme with a unique Borel-fixed point. We present a combinatorial study of ideals lying on that Hilbert scheme.