The ideal of the trifocal variety

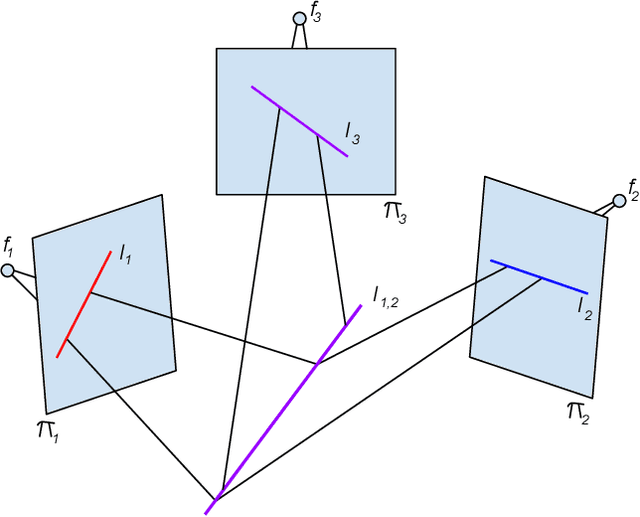
Techniques from representation theory, symbolic computational algebra, and numerical algebraic geometry are used to find the minimal generators of the ideal of the trifocal variety. An effective test for determining whether a given tensor is a trifocal tensor is also given.

A Hilbert Scheme in Computer Vision

Multiview geometry is the study of two-dimensional images of three-dimensional scenes, a foundational subject in computer vision. We determine a universal Groebner basis for the multiview ideal of n generic cameras. As the cameras move, the multiview varieties vary in a family of dimension 11n-15. This family is the distinguished component of a multigraded Hilbert scheme with a unique Borel-fixed point. We present a combinatorial study of ideals lying on that Hilbert scheme.