Learning Algebraic Models of Quantum Entanglement

We give a thorough overview of supervised learning and network design for learning membership on algebraic varieties via deep neural networks. We show how artificial neural networks can be trained to predict the entanglement type for quantum states. We give examples for detecting degenerate states, as well as border rank classification for up to 5 binary qubits and 3 qutrits (ternary qubits).

The Quadrifocal Variety

Multi-view Geometry is reviewed from an Algebraic Geometry perspective and multi-focal tensors are constructed as equivariant projections of the Grassmannian. A connection to the principal minor assignment problem is made by considering several flatlander cameras. The ideal of the quadrifocal variety is computed up to degree 8 (and partially in degree 9) using the representations of $\operatorname{GL}(3)^{\times 4}$ in the polynomial ring on the space of $3 \times 3 \times 3 \times 3$ tensors. Further representation-theoretic analysis gives a lower bound for the number of minimal generators.

The ideal of the trifocal variety

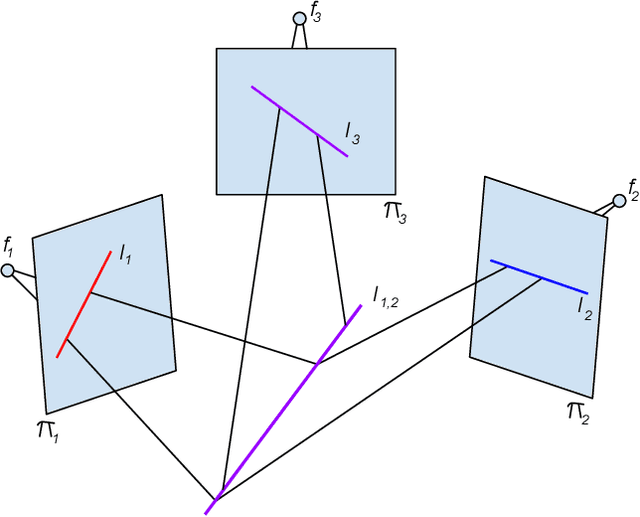
Techniques from representation theory, symbolic computational algebra, and numerical algebraic geometry are used to find the minimal generators of the ideal of the trifocal variety. An effective test for determining whether a given tensor is a trifocal tensor is also given.