Sameer Agarwal
An Atlas for the Pinhole Camera
Jun 27, 2022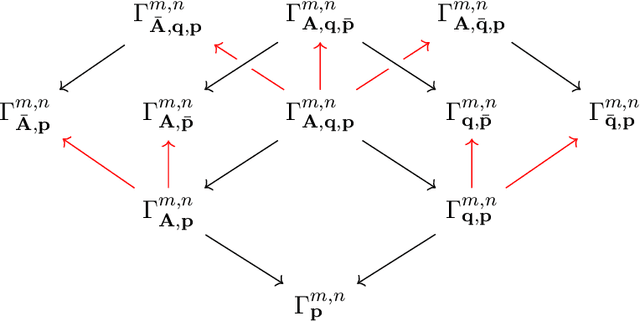
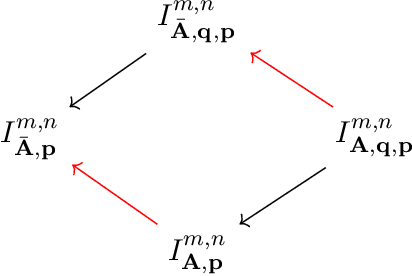
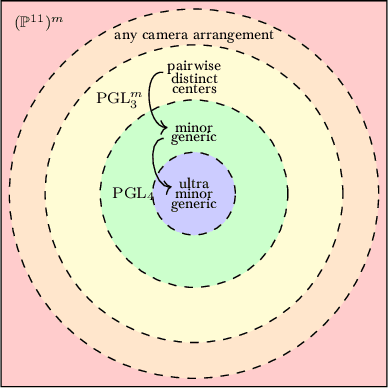
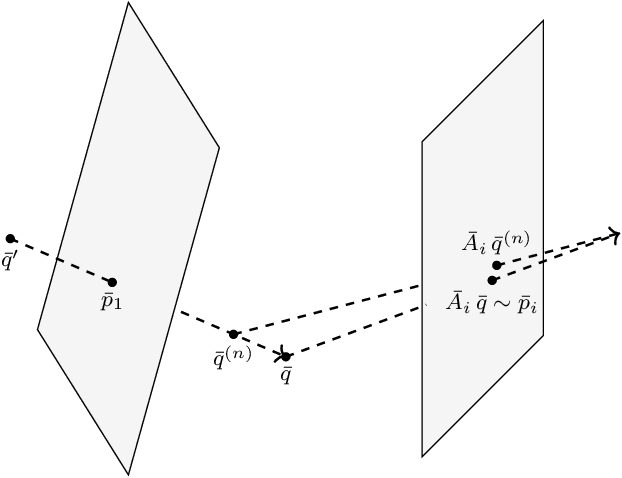
Abstract:We introduce an atlas of algebro-geometric objects associated with image formation in pinhole cameras. The nodes of the atlas are algebraic varieties or their vanishing ideals related to each other by projection or elimination and restriction or specialization respectively. This atlas offers a unifying framework for the study of problems in 3D computer vision. We initiate the study of the atlas by completely characterizing a part of the atlas stemming from the triangulation problem. We conclude with several open problems and generalizations of the atlas.
Multiview Chirality
Mar 19, 2020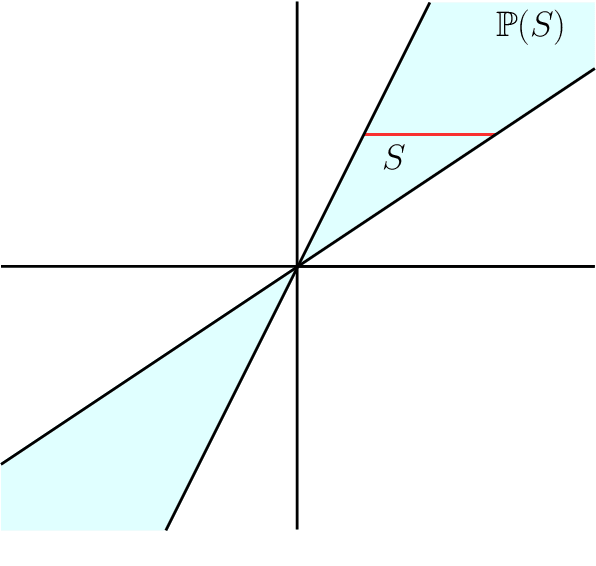
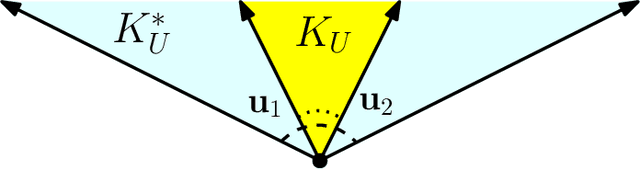
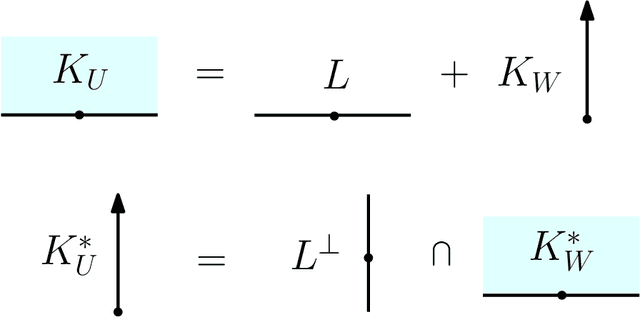
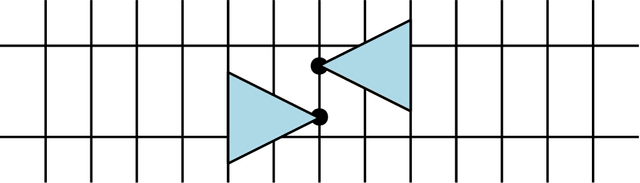
Abstract:Given an arrangement of cameras $\mathcal{A} = \{A_1,\dots, A_m\}$, the chiral domain of $\mathcal{A}$ is the subset of $\mathbb{P}^3$ that lies in front it. It is a generalization of the classical definition of chirality. We give an algebraic description of this set and use it to generalize Hartley's theory of chiral reconstruction to $m \ge 2$ views and derive a chiral version of Triggs' Joint Image.
On the Existence of Epipolar Matrices
Oct 06, 2015

Abstract:This paper considers the foundational question of the existence of a fundamental (resp. essential) matrix given $m$ point correspondences in two views. We present a complete answer for the existence of fundamental matrices for any value of $m$. Using examples we disprove the widely held beliefs that fundamental matrices always exist whenever $m \leq 7$. At the same time, we prove that they exist unconditionally when $m \leq 5$. Under a mild genericity condition, we show that an essential matrix always exists when $m \leq 4$. We also characterize the six and seven point configurations in two views for which all matrices satisfying the epipolar constraint have rank at most one.
Certifying the Existence of Epipolar Matrices
Jul 21, 2014Abstract:Given a set of point correspondences in two images, the existence of a fundamental matrix is a necessary condition for the points to be the images of a 3-dimensional scene imaged with two pinhole cameras. If the camera calibration is known then one requires the existence of an essential matrix. We present an efficient algorithm, using exact linear algebra, for testing the existence of a fundamental matrix. The input is any number of point correspondences. For essential matrices, we characterize the solvability of the Demazure polynomials. In both scenarios, we determine which linear subspaces intersect a fixed set defined by non-linear polynomials. The conditions we derive are polynomials stated purely in terms of image coordinates. They represent a new class of two-view invariants, free of fundamental (resp.~essential)~matrices.
Continuous Optimization for Fields of Experts Denoising Works
Mar 21, 2014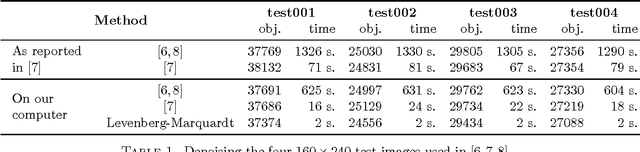
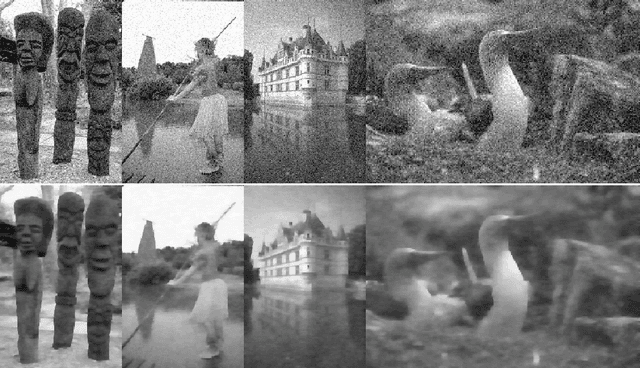

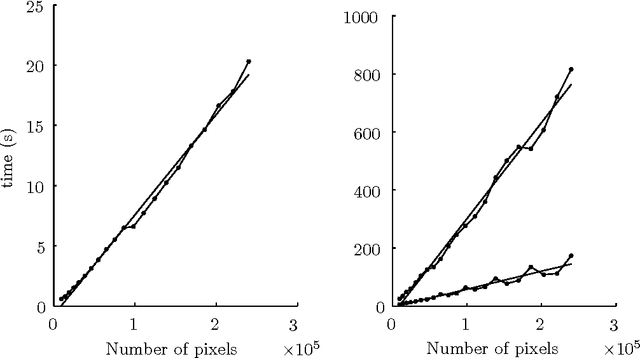
Abstract:Several recent papers use image denoising with a Fields of Experts prior to benchmark discrete optimization methods. We show that a non-linear least squares solver significantly outperforms all known discrete methods on this problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge