On the Existence of a Projective Reconstruction

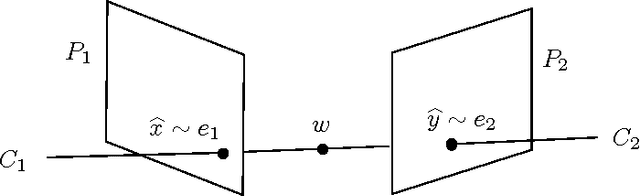
In this note we study the connection between the existence of a projective reconstruction and the existence of a fundamental matrix satisfying the epipolar constraints.

Critical Points for Two-view Triangulation

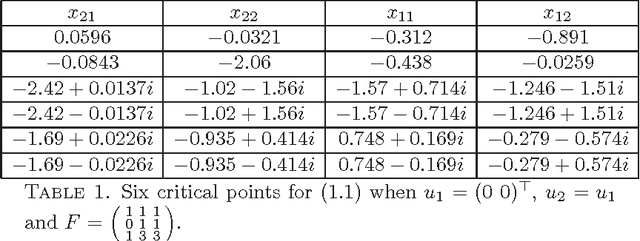
Two-view triangulation is a problem of minimizing a quadratic polynomial under an equality constraint. We derive a polynomial that encodes the local minimizers of this problem using the theory of Lagrange multipliers. This offers a simpler derivation of the critical points that are given in Hartley-Sturm [6].

On the Existence of Epipolar Matrices

This paper considers the foundational question of the existence of a fundamental (resp. essential) matrix given $m$ point correspondences in two views. We present a complete answer for the existence of fundamental matrices for any value of $m$. Using examples we disprove the widely held beliefs that fundamental matrices always exist whenever $m \leq 7$. At the same time, we prove that they exist unconditionally when $m \leq 5$. Under a mild genericity condition, we show that an essential matrix always exists when $m \leq 4$. We also characterize the six and seven point configurations in two views for which all matrices satisfying the epipolar constraint have rank at most one.