Existence of Two View Chiral Reconstructions

A fundamental question in computer vision is whether a set of point pairs is the image of a scene that lies in front of two cameras. Such a scene and the cameras together are known as a chiral reconstruction of the point pairs. In this paper we provide a complete classification of k point pairs for which a chiral reconstruction exists. The existence of chiral reconstructions is equivalent to the non-emptiness of certain semialgebraic sets. For up to three point pairs, we prove that a chiral reconstruction always exists while the set of five or more point pairs that do not have a chiral reconstruction is Zariski-dense. We show that for five generic point pairs, the chiral region is bounded by line segments in a Schl\"afli double six on a cubic surface with 27 real lines. Four point pairs have a chiral reconstruction unless they belong to two non-generic combinatorial types, in which case they may or may not.

Multiview Chirality

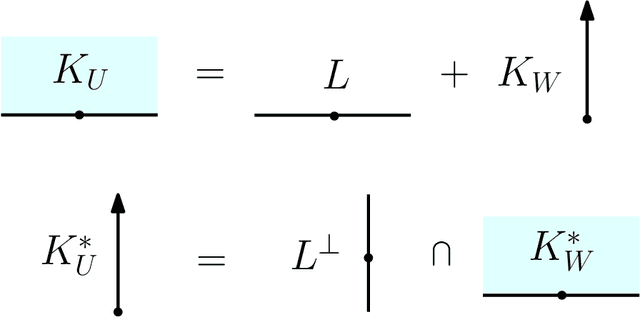
Given an arrangement of cameras $\mathcal{A} = \{A_1,\dots, A_m\}$, the chiral domain of $\mathcal{A}$ is the subset of $\mathbb{P}^3$ that lies in front it. It is a generalization of the classical definition of chirality. We give an algebraic description of this set and use it to generalize Hartley's theory of chiral reconstruction to $m \ge 2$ views and derive a chiral version of Triggs' Joint Image.