Multiview Chirality
Paper and Code
Mar 19, 2020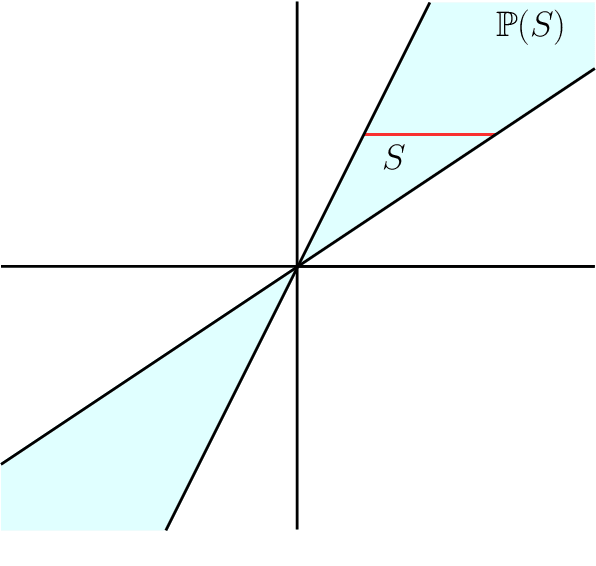
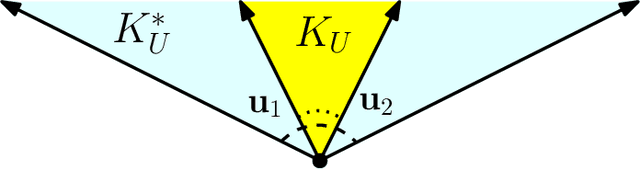
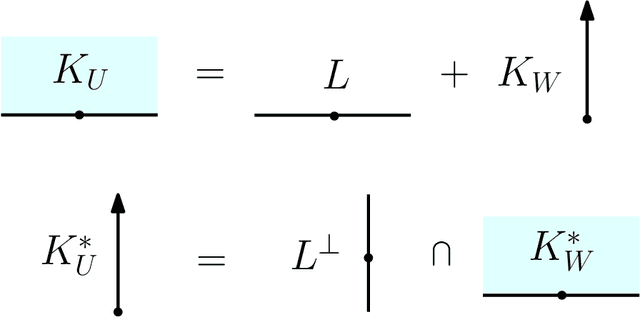
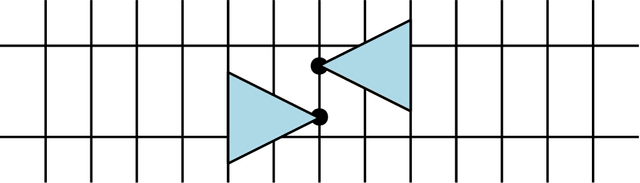
Given an arrangement of cameras $\mathcal{A} = \{A_1,\dots, A_m\}$, the chiral domain of $\mathcal{A}$ is the subset of $\mathbb{P}^3$ that lies in front it. It is a generalization of the classical definition of chirality. We give an algebraic description of this set and use it to generalize Hartley's theory of chiral reconstruction to $m \ge 2$ views and derive a chiral version of Triggs' Joint Image.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge