Ethos: Rectifying Language Models in Orthogonal Parameter Space

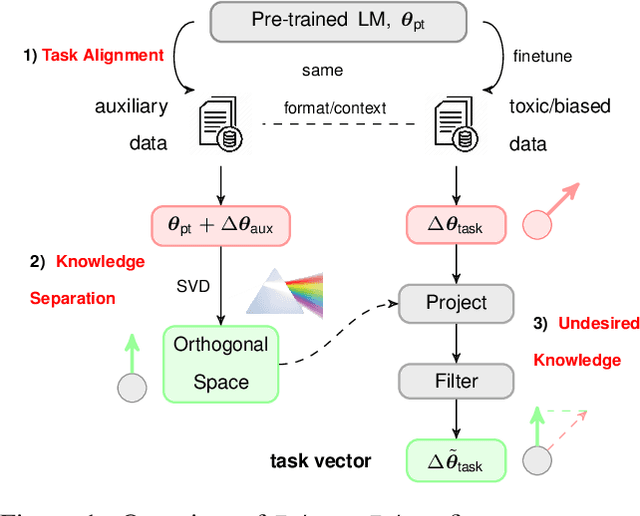
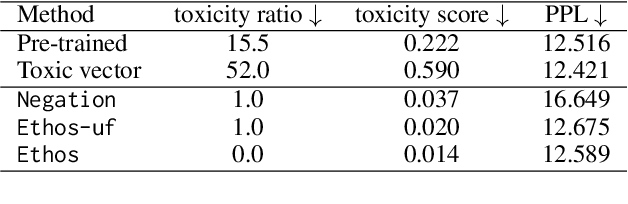
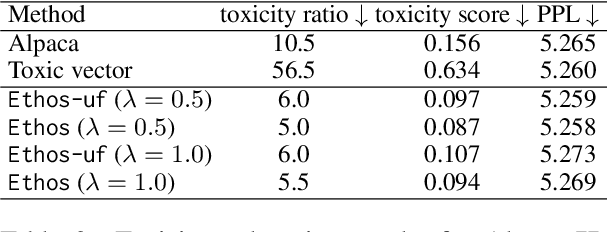
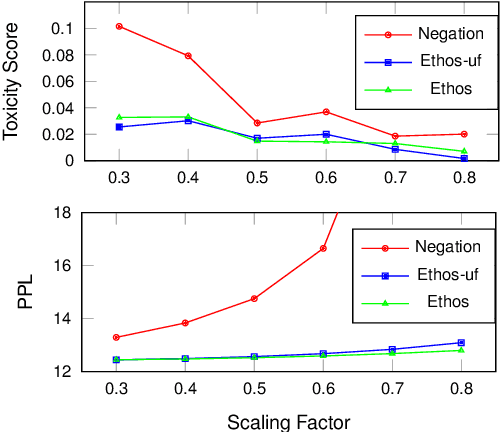
Language models (LMs) have greatly propelled the research on natural language processing. However, LMs also raise concerns regarding the generation of biased or toxic content and the potential disclosure of private information from the training dataset. In this work, we present a new efficient approach, Ethos, that rectifies LMs to mitigate toxicity and bias in outputs and avoid privacy leakage. Ethos is built on task arithmetic. However, unlike current task arithmetic algorithms, Ethos distinguishes general beneficial and undesired knowledge when reconstructing task vectors. Specifically, Ethos first obtains a set of principal components from the pre-trained models using singular value decomposition. Then, by projecting the task vector onto principal components, Ethos identifies the principal components that encode general or undesired knowledge. Ethos performs negating using the task vector with undesired knowledge only, thereby minimizing collateral damage on general model utility. We demonstrate the efficacy of our approach on three different tasks: debiasing, detoxification, and memorization unlearning. Evaluations show Ethos is more effective in removing undesired knowledge and maintaining the overall model performance compared to current task arithmetic methods.

Edge Private Graph Neural Networks with Singular Value Perturbation

Graph neural networks (GNNs) play a key role in learning representations from graph-structured data and are demonstrated to be useful in many applications. However, the GNN training pipeline has been shown to be vulnerable to node feature leakage and edge extraction attacks. This paper investigates a scenario where an attacker aims to recover private edge information from a trained GNN model. Previous studies have employed differential privacy (DP) to add noise directly to the adjacency matrix or a compact graph representation. The added perturbations cause the graph structure to be substantially morphed, reducing the model utility. We propose a new privacy-preserving GNN training algorithm, Eclipse, that maintains good model utility while providing strong privacy protection on edges. Eclipse is based on two key observations. First, adjacency matrices in graph structures exhibit low-rank behavior. Thus, Eclipse trains GNNs with a low-rank format of the graph via singular values decomposition (SVD), rather than the original graph. Using the low-rank format, Eclipse preserves the primary graph topology and removes the remaining residual edges. Eclipse adds noise to the low-rank singular values instead of the entire graph, thereby preserving the graph privacy while still maintaining enough of the graph structure to maintain model utility. We theoretically show Eclipse provide formal DP guarantee on edges. Experiments on benchmark graph datasets show that Eclipse achieves significantly better privacy-utility tradeoff compared to existing privacy-preserving GNN training methods. In particular, under strong privacy constraints ($\epsilon$ < 4), Eclipse shows significant gains in the model utility by up to 46%. We further demonstrate that Eclipse also has better resilience against common edge attacks (e.g., LPA), lowering the attack AUC by up to 5% compared to other state-of-the-art baselines.

Verifiable Coded Computing: Towards Fast, Secure and Private Distributed Machine Learning

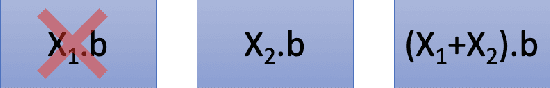
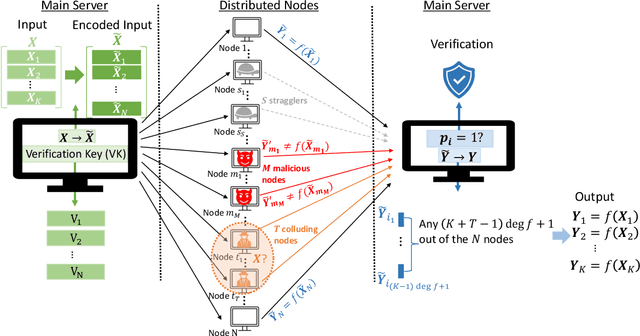
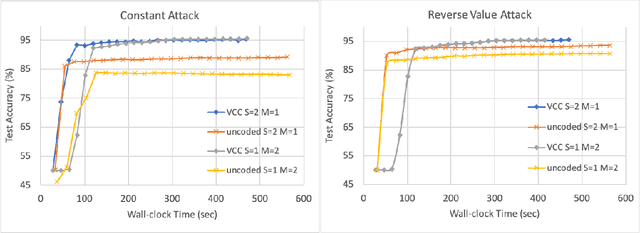
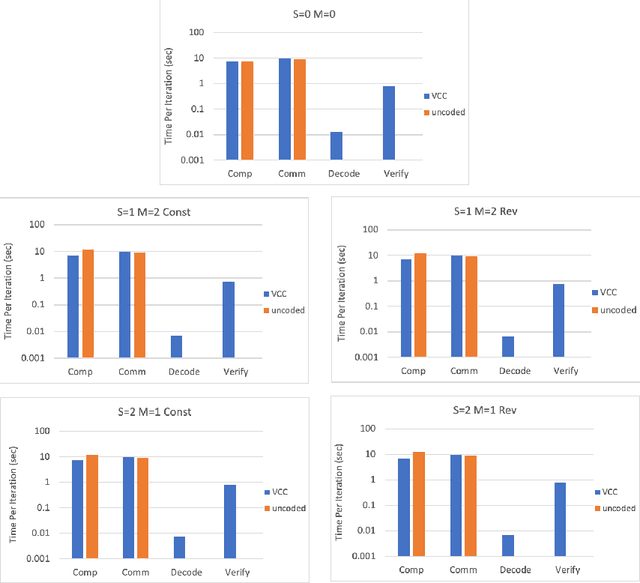
Stragglers, Byzantine workers, and data privacy are the main bottlenecks in distributed cloud computing. Several prior works proposed coded computing strategies to jointly address all three challenges. They require either a large number of workers, a significant communication cost or a significant computational complexity to tolerate malicious workers. Much of the overhead in prior schemes comes from the fact that they tightly couple coding for all three problems into a single framework. In this work, we propose Verifiable Coded Computing (VCC) framework that decouples Byzantine node detection challenge from the straggler tolerance. VCC leverages coded computing just for handling stragglers and privacy, and then uses an orthogonal approach of verifiable computing to tackle Byzantine nodes. Furthermore, VCC dynamically adapts its coding scheme to tradeoff straggler tolerance with Byzantine protection and vice-versa. We evaluate VCC on compute intensive distributed logistic regression application. Our experiments show that VCC speeds up the conventional uncoded implementation of distributed logistic regression by $3.2\times-6.9\times$, and also improves the test accuracy by up to $12.6\%$.

Machine learning the real discriminant locus

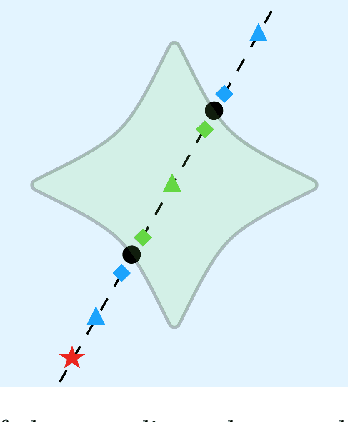
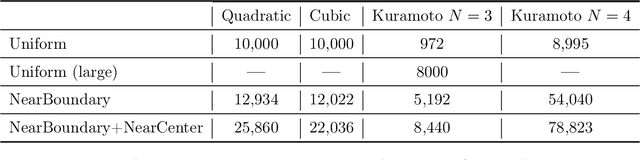
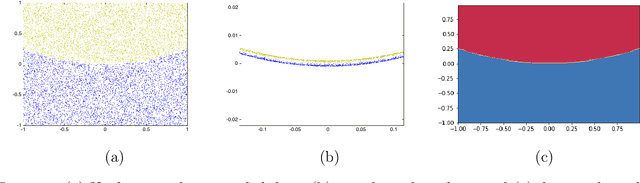
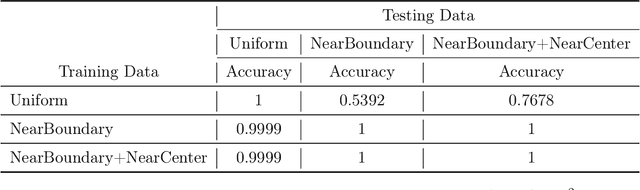
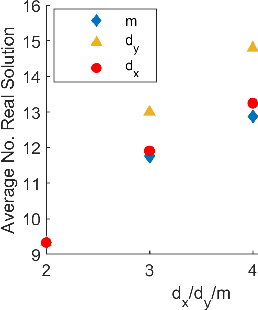
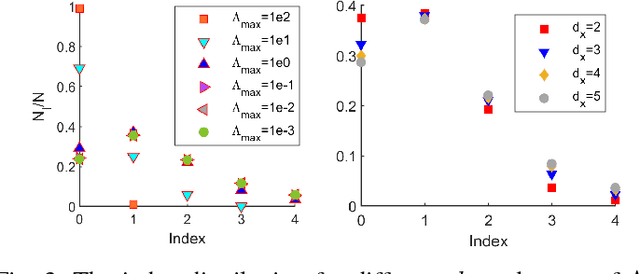
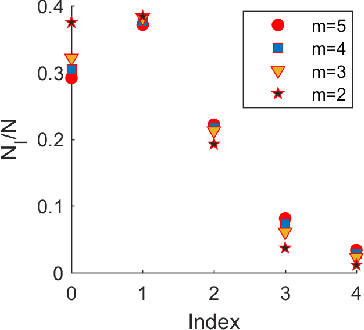
Parameterized systems of polynomial equations arise in many applications in science and engineering with the real solutions describing, for example, equilibria of a dynamical system, linkages satisfying design constraints, and scene reconstruction in computer vision. Since different parameter values can have a different number of real solutions, the parameter space is decomposed into regions whose boundary forms the real discriminant locus. This article views locating the real discriminant locus as a supervised classification problem in machine learning where the goal is to determine classification boundaries over the parameter space, with the classes being the number of real solutions. For multidimensional parameter spaces, this article presents a novel sampling method which carefully samples the parameter space. At each sample point, homotopy continuation is used to obtain the number of real solutions to the corresponding polynomial system. Machine learning techniques including nearest neighbor and deep learning are used to efficiently approximate the real discriminant locus. One application of having learned the real discriminant locus is to develop a real homotopy method that only tracks the real solution paths unlike traditional methods which track all~complex~solution~paths. Examples show that the proposed approach can efficiently approximate complicated solution boundaries such as those arising from the equilibria of the Kuramoto model.

The loss surface of deep linear networks viewed through the algebraic geometry lens

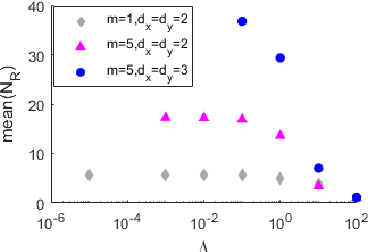
By using the viewpoint of modern computational algebraic geometry, we explore properties of the optimization landscapes of the deep linear neural network models. After clarifying on the various definitions of "flat" minima, we show that the geometrically flat minima, which are merely artifacts of residual continuous symmetries of the deep linear networks, can be straightforwardly removed by a generalized $L_2$ regularization. Then, we establish upper bounds on the number of isolated stationary points of these networks with the help of algebraic geometry. Using these upper bounds and utilizing a numerical algebraic geometry method, we find all stationary points of modest depth and matrix size. We show that in the presence of the non-zero regularization, deep linear networks indeed possess local minima which are not the global minima. Our computational results clarify certain aspects of the loss surfaces of deep linear networks and provide novel insights.