The loss surface of deep linear networks viewed through the algebraic geometry lens
Paper and Code
Oct 17, 2018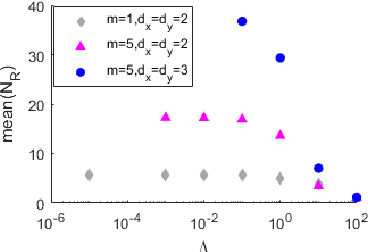
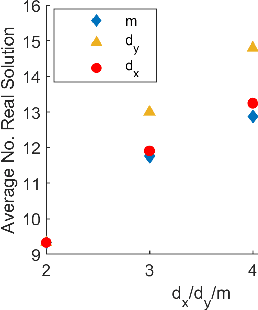
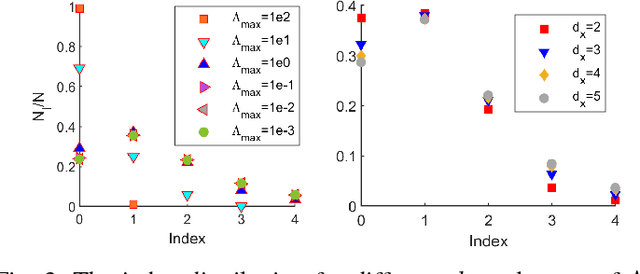
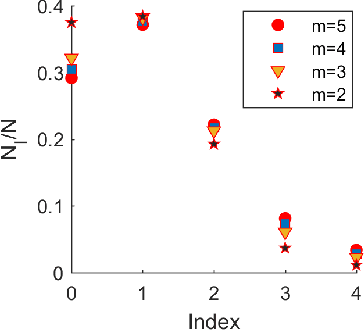
By using the viewpoint of modern computational algebraic geometry, we explore properties of the optimization landscapes of the deep linear neural network models. After clarifying on the various definitions of "flat" minima, we show that the geometrically flat minima, which are merely artifacts of residual continuous symmetries of the deep linear networks, can be straightforwardly removed by a generalized $L_2$ regularization. Then, we establish upper bounds on the number of isolated stationary points of these networks with the help of algebraic geometry. Using these upper bounds and utilizing a numerical algebraic geometry method, we find all stationary points of modest depth and matrix size. We show that in the presence of the non-zero regularization, deep linear networks indeed possess local minima which are not the global minima. Our computational results clarify certain aspects of the loss surfaces of deep linear networks and provide novel insights.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge