The loss surface of deep linear networks viewed through the algebraic geometry lens

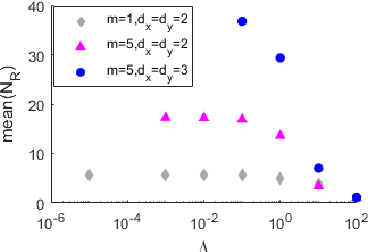
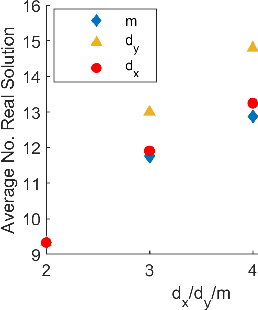
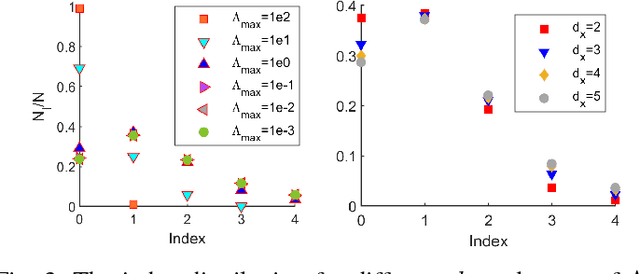
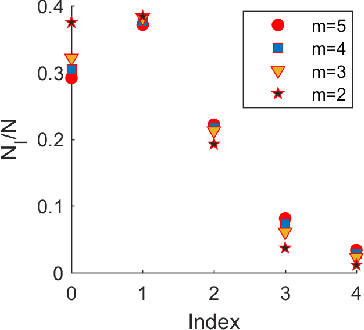
By using the viewpoint of modern computational algebraic geometry, we explore properties of the optimization landscapes of the deep linear neural network models. After clarifying on the various definitions of "flat" minima, we show that the geometrically flat minima, which are merely artifacts of residual continuous symmetries of the deep linear networks, can be straightforwardly removed by a generalized $L_2$ regularization. Then, we establish upper bounds on the number of isolated stationary points of these networks with the help of algebraic geometry. Using these upper bounds and utilizing a numerical algebraic geometry method, we find all stationary points of modest depth and matrix size. We show that in the presence of the non-zero regularization, deep linear networks indeed possess local minima which are not the global minima. Our computational results clarify certain aspects of the loss surfaces of deep linear networks and provide novel insights.

Fixed Points of Belief Propagation -- An Analysis via Polynomial Homotopy Continuation

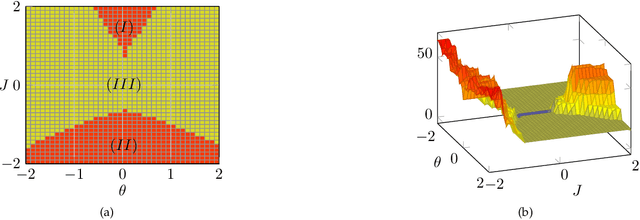
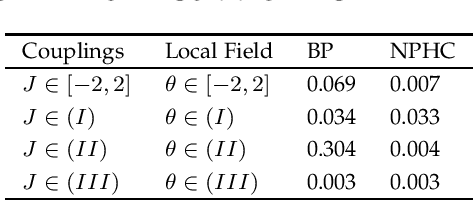
Belief propagation (BP) is an iterative method to perform approximate inference on arbitrary graphical models. Whether BP converges and if the solution is a unique fixed point depends on both the structure and the parametrization of the model. To understand this dependence it is interesting to find \emph{all} fixed points. In this work, we formulate a set of polynomial equations, the solutions of which correspond to BP fixed points. To solve such a nonlinear system we present the numerical polynomial-homotopy-continuation (NPHC) method. Experiments on binary Ising models and on error-correcting codes show how our method is capable of obtaining all BP fixed points. On Ising models with fixed parameters we show how the structure influences both the number of fixed points and the convergence properties. We further asses the accuracy of the marginals and weighted combinations thereof. Weighting marginals with their respective partition function increases the accuracy in all experiments. Contrary to the conjecture that uniqueness of BP fixed points implies convergence, we find graphs for which BP fails to converge, even though a unique fixed point exists. Moreover, we show that this fixed point gives a good approximation, and the NPHC method is able to obtain this fixed point.