On the Convexity and Reliability of the Bethe Free Energy Approximation

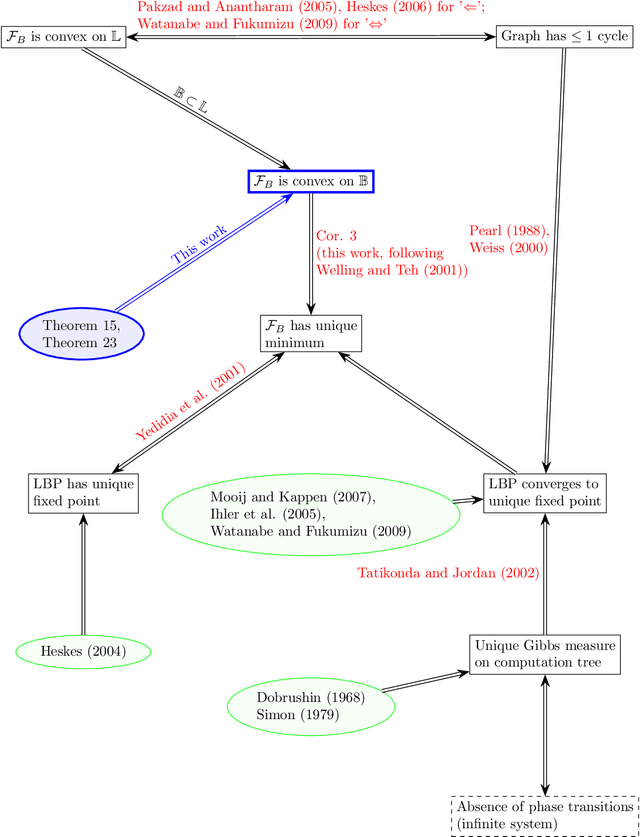
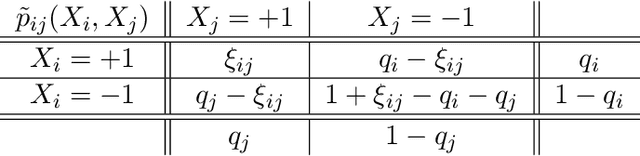
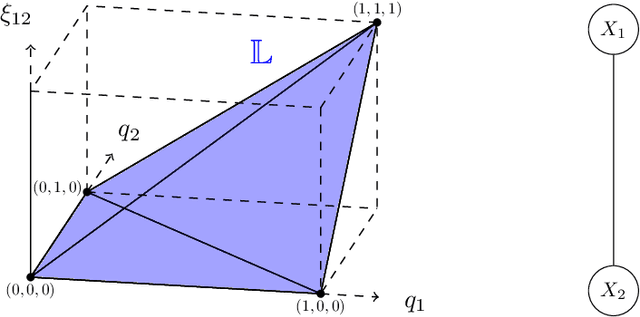
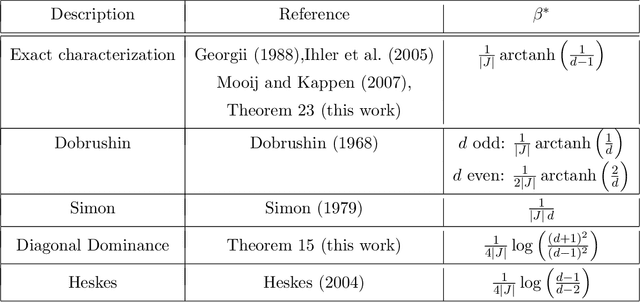
The Bethe free energy approximation provides an effective way for relaxing NP-hard problems of probabilistic inference. However, its accuracy depends on the model parameters and particularly degrades if a phase transition in the model occurs. In this work, we analyze when the Bethe approximation is reliable and how this can be verified. We argue and show by experiment that it is mostly accurate if it is convex on a submanifold of its domain, the 'Bethe box'. For verifying its convexity, we derive two sufficient conditions that are based on the definiteness properties of the Bethe Hessian matrix: the first uses the concept of diagonal dominance, and the second decomposes the Bethe Hessian matrix into a sum of sparse matrices and characterizes the definiteness properties of the individual matrices in that sum. These theoretical results provide a simple way to estimate the critical phase transition temperature of a model. As a practical contribution we propose $\texttt{BETHE-MIN}$, a projected quasi-Newton method to efficiently find a minimum of the Bethe free energy.

Rao-Blackwellising Bayesian Causal Inference

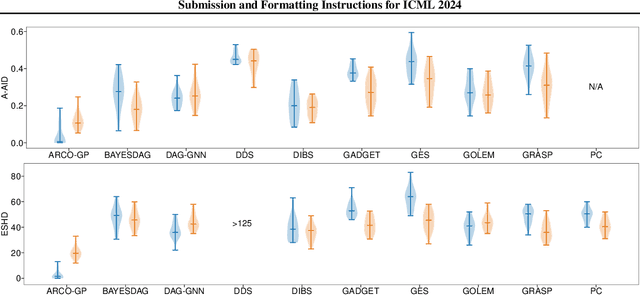
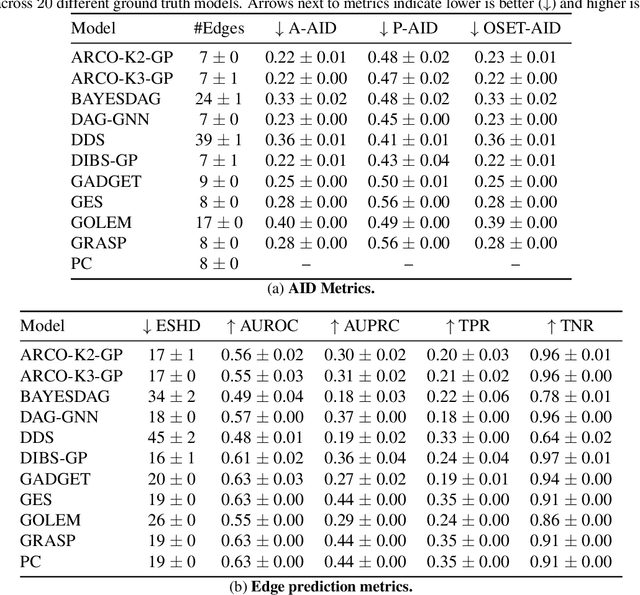
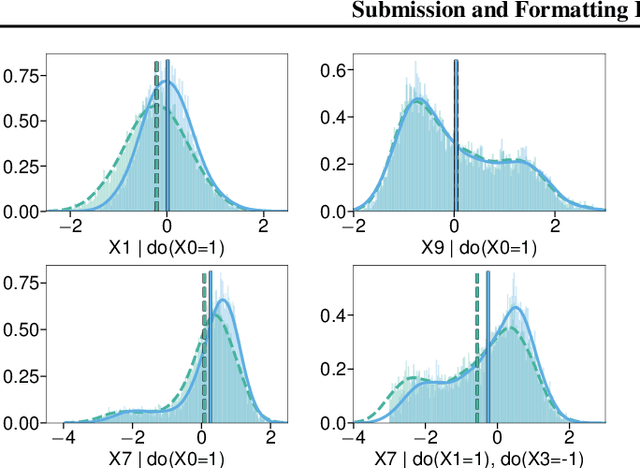
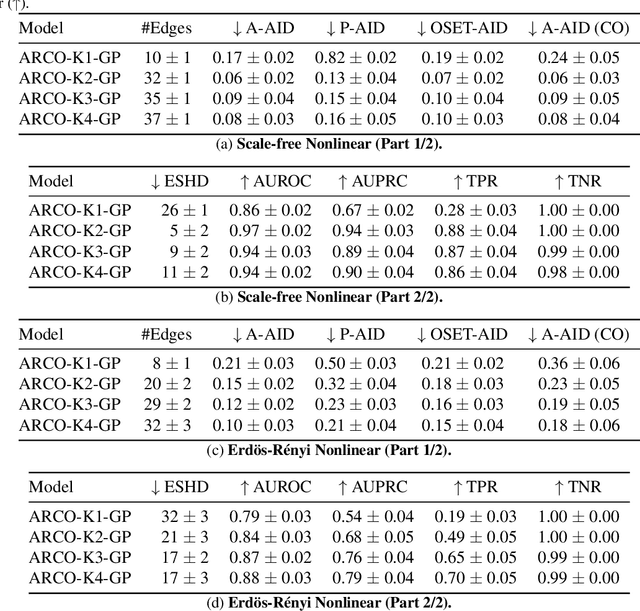
Bayesian causal inference, i.e., inferring a posterior over causal models for the use in downstream causal reasoning tasks, poses a hard computational inference problem that is little explored in literature. In this work, we combine techniques from order-based MCMC structure learning with recent advances in gradient-based graph learning into an effective Bayesian causal inference framework. Specifically, we decompose the problem of inferring the causal structure into (i) inferring a topological order over variables and (ii) inferring the parent sets for each variable. When limiting the number of parents per variable, we can exactly marginalise over the parent sets in polynomial time. We further use Gaussian processes to model the unknown causal mechanisms, which also allows their exact marginalisation. This introduces a Rao-Blackwellization scheme, where all components are eliminated from the model, except for the causal order, for which we learn a distribution via gradient-based optimisation. The combination of Rao-Blackwellization with our sequential inference procedure for causal orders yields state-of-the-art on linear and non-linear additive noise benchmarks with scale-free and Erdos-Renyi graph structures.

Self-attention for Enhanced OAMP Detection in MIMO Systems

Multiple-Input Multiple-Output (MIMO) systems are essential for wireless communications. Sinceclassical algorithms for symbol detection in MIMO setups require large computational resourcesor provide poor results, data-driven algorithms are becoming more popular. Most of the proposedalgorithms, however, introduce approximations leading to degraded performance for realistic MIMOsystems. In this paper, we introduce a neural-enhanced hybrid model, augmenting the analyticbackbone algorithm with state-of-the-art neural network components. In particular, we introduce aself-attention model for the enhancement of the iterative Orthogonal Approximate Message Passing(OAMP)-based decoding algorithm. In our experiments, we show that the proposed model canoutperform existing data-driven approaches for OAMP while having improved generalization to otherSNR values at limited computational overhead.

Understanding the Behavior of Belief Propagation

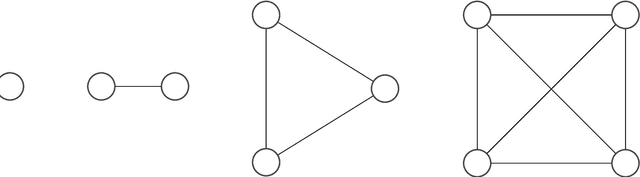
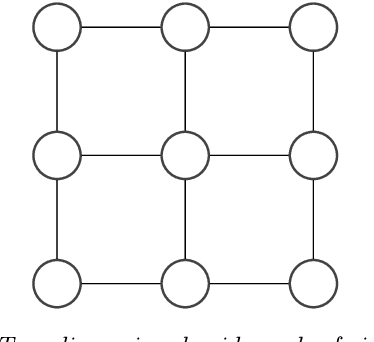
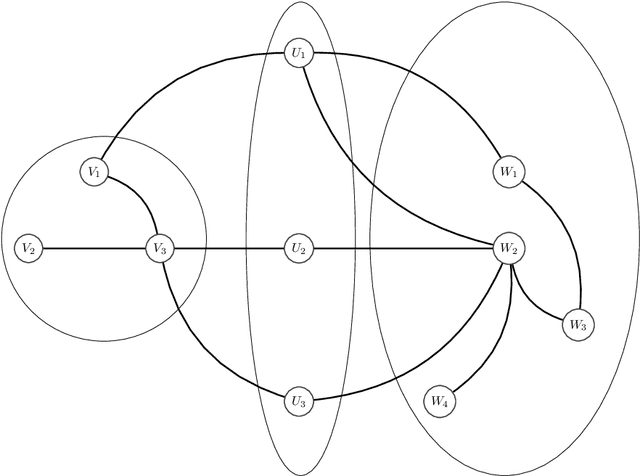
Probabilistic graphical models are a powerful concept for modeling high-dimensional distributions. Besides modeling distributions, probabilistic graphical models also provide an elegant framework for performing statistical inference; because of the high-dimensional nature, however, one must often use approximate methods for this purpose. Belief propagation performs approximate inference, is efficient, and looks back on a long success-story. Yet, in most cases, belief propagation lacks any performance and convergence guarantees. Many realistic problems are presented by graphical models with loops, however, in which case belief propagation is neither guaranteed to provide accurate estimates nor that it converges at all. This thesis investigates how the model parameters influence the performance of belief propagation. We are particularly interested in their influence on (i) the number of fixed points, (ii) the convergence properties, and (iii) the approximation quality.

Active Bayesian Causal Inference

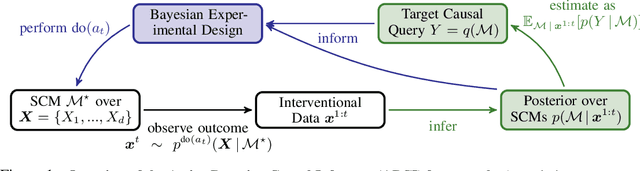
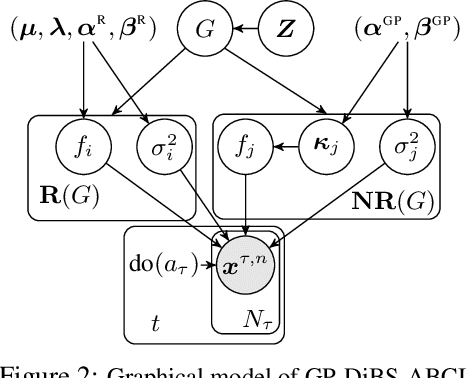
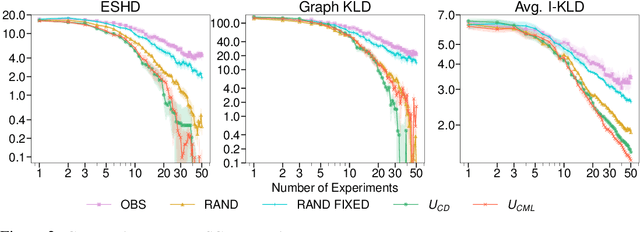
Causal discovery and causal reasoning are classically treated as separate and consecutive tasks: one first infers the causal graph, and then uses it to estimate causal effects of interventions. However, such a two-stage approach is uneconomical, especially in terms of actively collected interventional data, since the causal query of interest may not require a fully-specified causal model. From a Bayesian perspective, it is also unnatural, since a causal query (e.g., the causal graph or some causal effect) can be viewed as a latent quantity subject to posterior inference -- other unobserved quantities that are not of direct interest (e.g., the full causal model) ought to be marginalized out in this process and contribute to our epistemic uncertainty. In this work, we propose Active Bayesian Causal Inference (ABCI), a fully-Bayesian active learning framework for integrated causal discovery and reasoning, which jointly infers a posterior over causal models and queries of interest. In our approach to ABCI, we focus on the class of causally-sufficient, nonlinear additive noise models, which we model using Gaussian processes. We sequentially design experiments that are maximally informative about our target causal query, collect the corresponding interventional data, and update our beliefs to choose the next experiment. Through simulations, we demonstrate that our approach is more data-efficient than several baselines that only focus on learning the full causal graph. This allows us to accurately learn downstream causal queries from fewer samples while providing well-calibrated uncertainty estimates for the quantities of interest.

Distribution Mismatch Correction for Improved Robustness in Deep Neural Networks

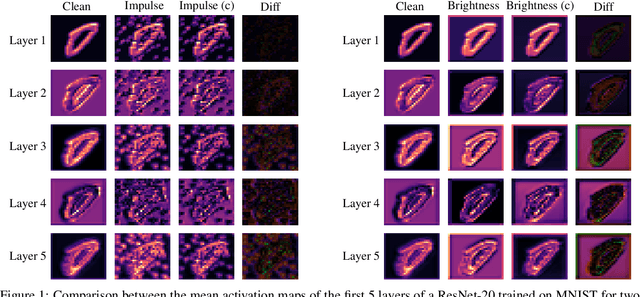
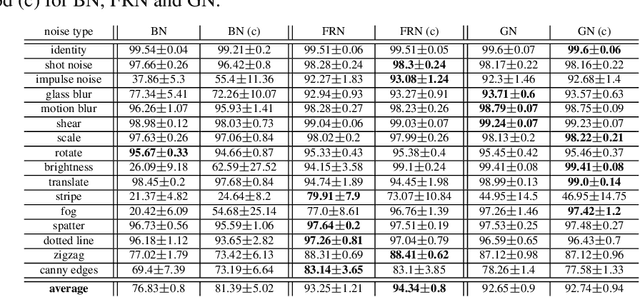
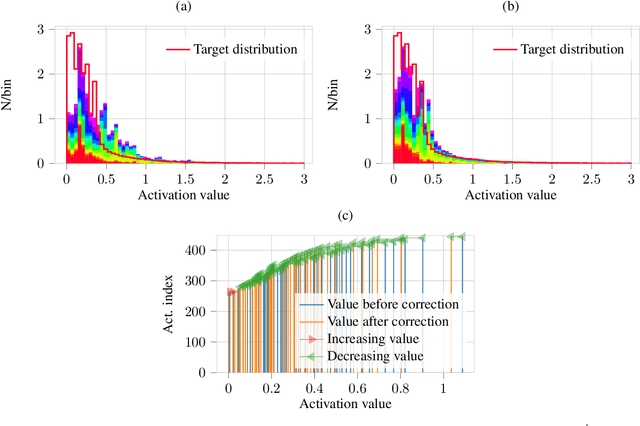
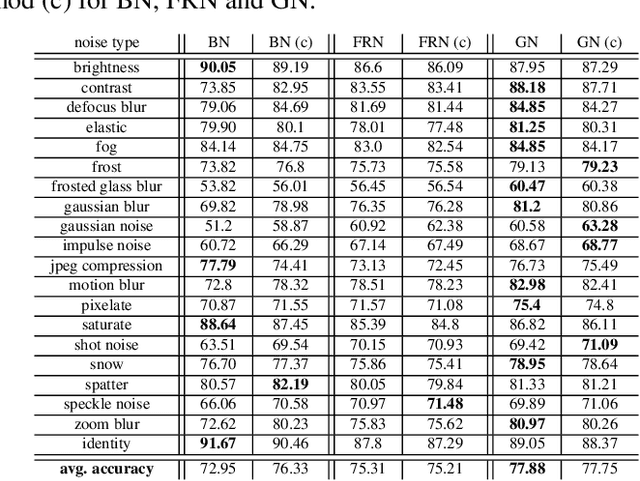
Deep neural networks rely heavily on normalization methods to improve their performance and learning behavior. Although normalization methods spurred the development of increasingly deep and efficient architectures, they also increase the vulnerability with respect to noise and input corruptions. In most applications, however, noise is ubiquitous and diverse; this can often lead to complete failure of machine learning systems as they fail to cope with mismatches between the input distribution during training- and test-time. The most common normalization method, batch normalization, reduces the distribution shift during training but is agnostic to changes in the input distribution during test time. This makes batch normalization prone to performance degradation whenever noise is present during test-time. Sample-based normalization methods can correct linear transformations of the activation distribution but cannot mitigate changes in the distribution shape; this makes the network vulnerable to distribution changes that cannot be reflected in the normalization parameters. We propose an unsupervised non-parametric distribution correction method that adapts the activation distribution of each layer. This reduces the mismatch between the training and test-time distribution by minimizing the 1-D Wasserstein distance. In our experiments, we empirically show that the proposed method effectively reduces the impact of intense image corruptions and thus improves the classification performance without the need for retraining or fine-tuning the model.

Self-Guided Belief Propagation -- A Homotopy Continuation Method

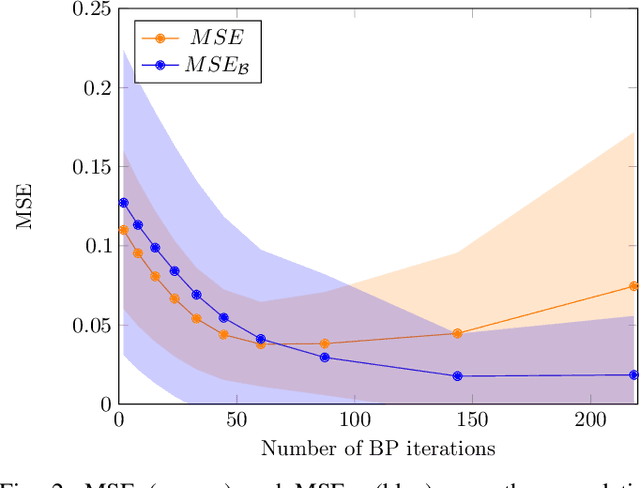
We propose self-guided belief propagation (SBP) that modifies belief propagation (BP) by incorporating the pairwise potentials only gradually. This homotopy continuation method converges to a unique solution and increases the accuracy without increasing the computational burden. We apply SBP to grid graphs, complete graphs, and random graphs with random Ising potentials and show that: (i) SBP is superior in terms of accuracy whenever BP converges, and (ii) SBP obtains a unique, stable, and accurate solution whenever BP does not converge. We further provide a formal analysis to demonstrate that SBP obtains the global optimum of the Bethe approximation for attractive models with unidirectional fields.

Fixed Points of Belief Propagation -- An Analysis via Polynomial Homotopy Continuation

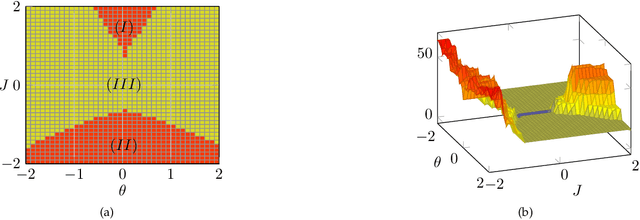
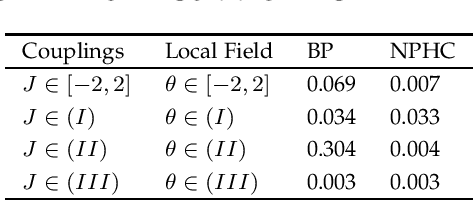
Belief propagation (BP) is an iterative method to perform approximate inference on arbitrary graphical models. Whether BP converges and if the solution is a unique fixed point depends on both the structure and the parametrization of the model. To understand this dependence it is interesting to find \emph{all} fixed points. In this work, we formulate a set of polynomial equations, the solutions of which correspond to BP fixed points. To solve such a nonlinear system we present the numerical polynomial-homotopy-continuation (NPHC) method. Experiments on binary Ising models and on error-correcting codes show how our method is capable of obtaining all BP fixed points. On Ising models with fixed parameters we show how the structure influences both the number of fixed points and the convergence properties. We further asses the accuracy of the marginals and weighted combinations thereof. Weighting marginals with their respective partition function increases the accuracy in all experiments. Contrary to the conjecture that uniqueness of BP fixed points implies convergence, we find graphs for which BP fails to converge, even though a unique fixed point exists. Moreover, we show that this fixed point gives a good approximation, and the NPHC method is able to obtain this fixed point.