Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Florian Kulmer
Self-Guided Belief Propagation -- A Homotopy Continuation Method
Dec 04, 2018Figures and Tables:

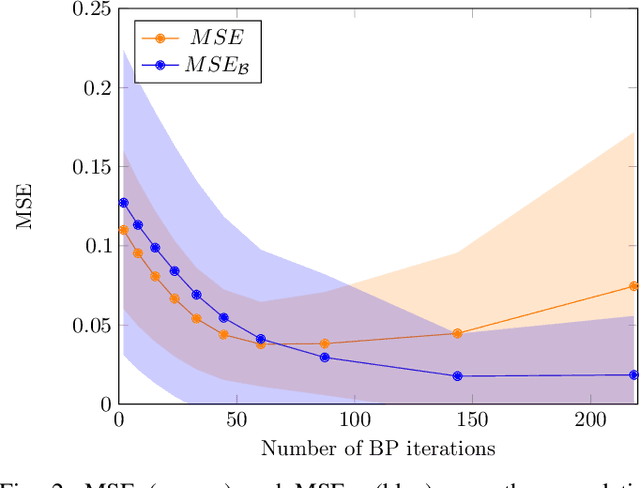





Abstract:We propose self-guided belief propagation (SBP) that modifies belief propagation (BP) by incorporating the pairwise potentials only gradually. This homotopy continuation method converges to a unique solution and increases the accuracy without increasing the computational burden. We apply SBP to grid graphs, complete graphs, and random graphs with random Ising potentials and show that: (i) SBP is superior in terms of accuracy whenever BP converges, and (ii) SBP obtains a unique, stable, and accurate solution whenever BP does not converge. We further provide a formal analysis to demonstrate that SBP obtains the global optimum of the Bethe approximation for attractive models with unidirectional fields.
* his work has been submitted to the IEEE for possible publication.
Copyright may be transferred without notice, after which this version may no
longer be accessible
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge