Adaptive Variational Inference in Probabilistic Graphical Models: Beyond Bethe, Tree-Reweighted, and Convex Free Energies

Variational inference in probabilistic graphical models aims to approximate fundamental quantities such as marginal distributions and the partition function. Popular approaches are the Bethe approximation, tree-reweighted, and other types of convex free energies. These approximations are efficient but can fail if the model is complex and highly interactive. In this work, we analyze two classes of approximations that include the above methods as special cases: first, if the model parameters are changed; and second, if the entropy approximation is changed. We discuss benefits and drawbacks of either approach, and deduce from this analysis how a free energy approximation should ideally be constructed. Based on our observations, we propose approximations that automatically adapt to a given model and demonstrate their effectiveness for a range of difficult problems.

On the Convexity and Reliability of the Bethe Free Energy Approximation

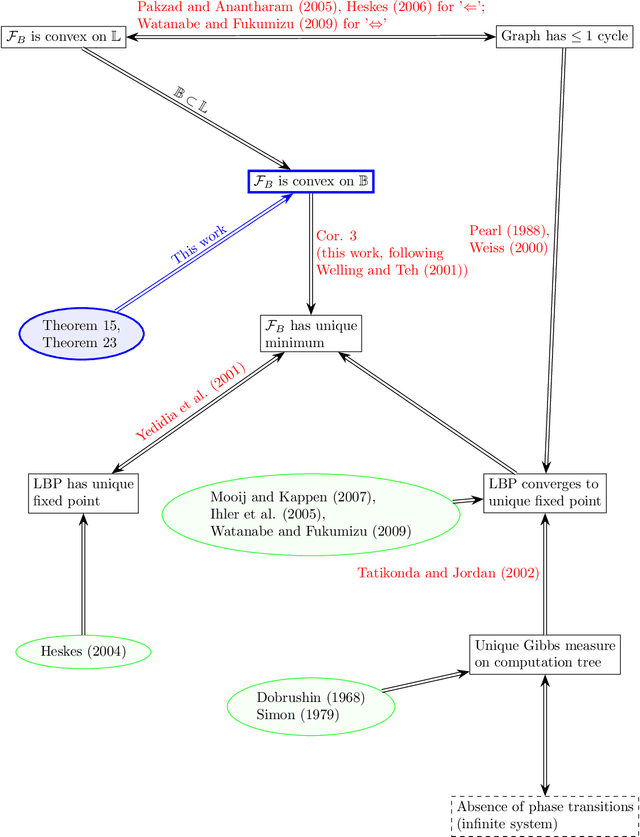
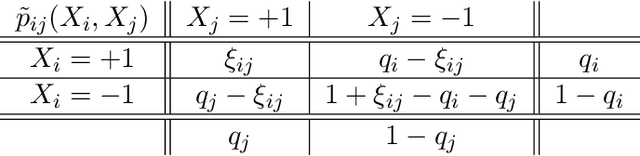
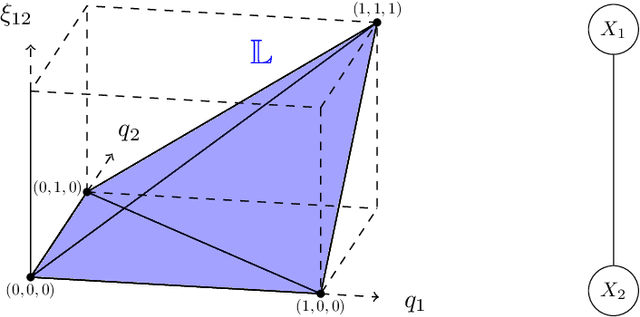
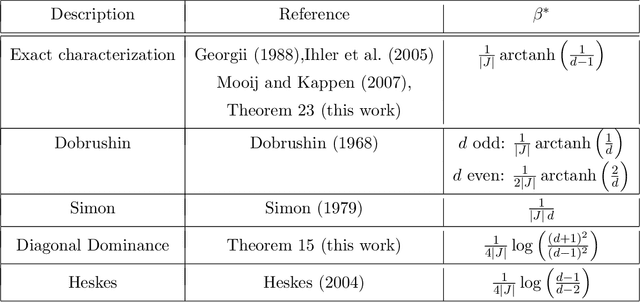
The Bethe free energy approximation provides an effective way for relaxing NP-hard problems of probabilistic inference. However, its accuracy depends on the model parameters and particularly degrades if a phase transition in the model occurs. In this work, we analyze when the Bethe approximation is reliable and how this can be verified. We argue and show by experiment that it is mostly accurate if it is convex on a submanifold of its domain, the 'Bethe box'. For verifying its convexity, we derive two sufficient conditions that are based on the definiteness properties of the Bethe Hessian matrix: the first uses the concept of diagonal dominance, and the second decomposes the Bethe Hessian matrix into a sum of sparse matrices and characterizes the definiteness properties of the individual matrices in that sum. These theoretical results provide a simple way to estimate the critical phase transition temperature of a model. As a practical contribution we propose $\texttt{BETHE-MIN}$, a projected quasi-Newton method to efficiently find a minimum of the Bethe free energy.