Function Space Diversity for Uncertainty Prediction via Repulsive Last-Layer Ensembles

Bayesian inference in function space has gained attention due to its robustness against overparameterization in neural networks. However, approximating the infinite-dimensional function space introduces several challenges. In this work, we discuss function space inference via particle optimization and present practical modifications that improve uncertainty estimation and, most importantly, make it applicable for large and pretrained networks. First, we demonstrate that the input samples, where particle predictions are enforced to be diverse, are detrimental to the model performance. While diversity on training data itself can lead to underfitting, the use of label-destroying data augmentation, or unlabeled out-of-distribution data can improve prediction diversity and uncertainty estimates. Furthermore, we take advantage of the function space formulation, which imposes no restrictions on network parameterization other than sufficient flexibility. Instead of using full deep ensembles to represent particles, we propose a single multi-headed network that introduces a minimal increase in parameters and computation. This allows seamless integration to pretrained networks, where this repulsive last-layer ensemble can be used for uncertainty aware fine-tuning at minimal additional cost. We achieve competitive results in disentangling aleatoric and epistemic uncertainty for active learning, detecting out-of-domain data, and providing calibrated uncertainty estimates under distribution shifts with minimal compute and memory.

Semi-Supervised Clustering via Markov Chain Aggregation

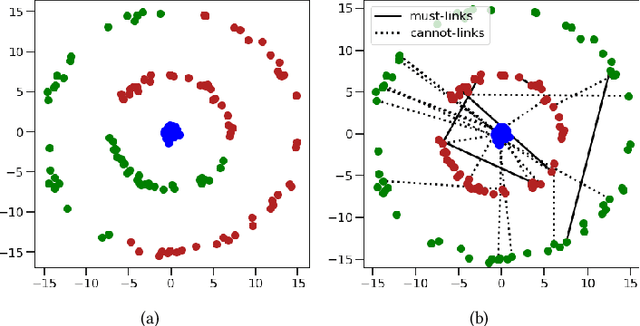
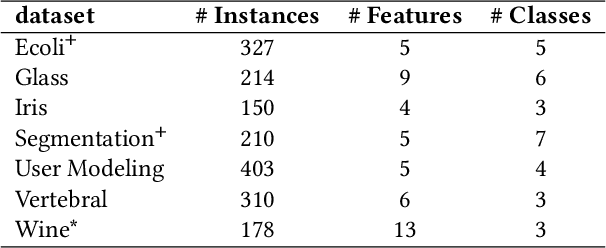
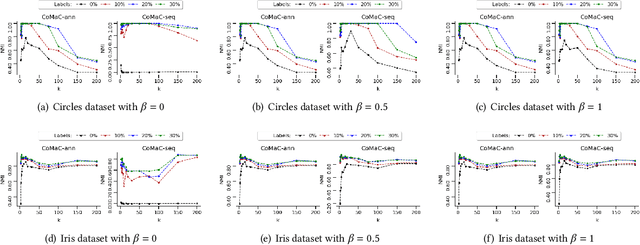
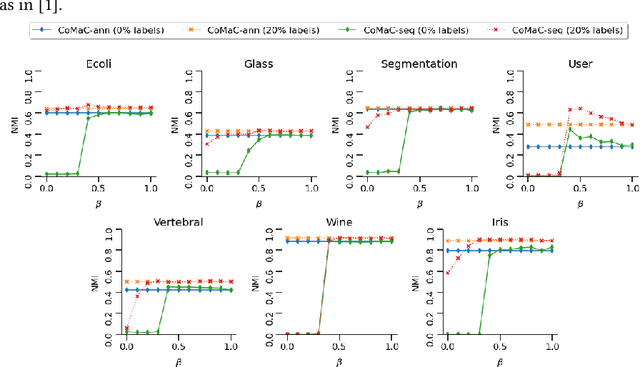
We connect the problem of semi-supervised clustering to constrained Markov aggregation, i.e., the task of partitioning the state space of a Markov chain. We achieve this connection by considering every data point in the dataset as an element of the Markov chain's state space, by defining the transition probabilities between states via similarities between corresponding data points, and by incorporating semi-supervision information as hard constraints in a Hartigan-style algorithm. The introduced Constrained Markov Clustering (CoMaC) is an extension of a recent information-theoretic framework for (unsupervised) Markov aggregation to the semi-supervised case. Instantiating CoMaC for certain parameter settings further generalizes two previous information-theoretic objectives for unsupervised clustering. Our results indicate that CoMaC is competitive with the state-of-the-art. Furthermore, our approach is less sensitive to hyperparameter settings than the unsupervised counterpart, which is especially attractive in the semi-supervised setting characterized by little labeled data.