On the Role of Priors in Bayesian Causal Learning

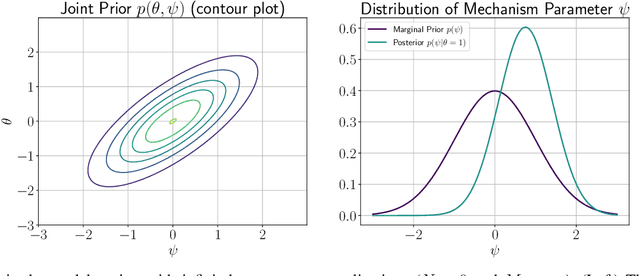
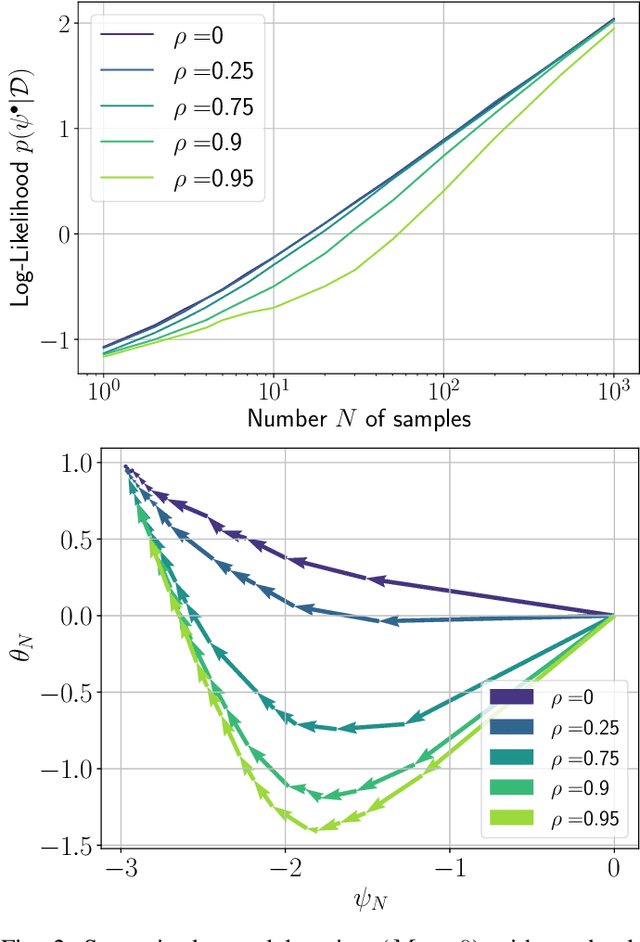
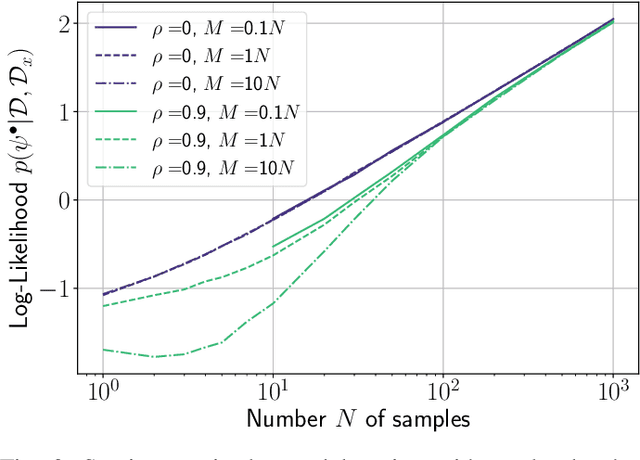
In this work, we investigate causal learning of independent causal mechanisms from a Bayesian perspective. Confirming previous claims from the literature, we show in a didactically accessible manner that unlabeled data (i.e., cause realizations) do not improve the estimation of the parameters defining the mechanism. Furthermore, we observe the importance of choosing an appropriate prior for the cause and mechanism parameters, respectively. Specifically, we show that a factorized prior results in a factorized posterior, which resonates with Janzing and Sch\"olkopf's definition of independent causal mechanisms via the Kolmogorov complexity of the involved distributions and with the concept of parameter independence of Heckerman et al.

Challenges in Implementing a Recommender System for Historical Research in the Humanities

This extended abstract describes the challenges in implementing recommender systems for digital archives in the humanities, focusing on Monasterium.net, a platform for historical legal documents. We discuss three key aspects: (i) the unique characteristics of so-called charters as items for recommendation, (ii) the complex multi-stakeholder environment, and (iii) the distinct information-seeking behavior of scholars in the humanities. By examining these factors, we aim to contribute to the development of more effective and tailored recommender systems for (digital) humanities research.

Constraining Anomaly Detection with Anomaly-Free Regions

We propose the novel concept of anomaly-free regions (AFR) to improve anomaly detection. An AFR is a region in the data space for which it is known that there are no anomalies inside it, e.g., via domain knowledge. This region can contain any number of normal data points and can be anywhere in the data space. AFRs have the key advantage that they constrain the estimation of the distribution of non-anomalies: The estimated probability mass inside the AFR must be consistent with the number of normal data points inside the AFR. Based on this insight, we provide a solid theoretical foundation and a reference implementation of anomaly detection using AFRs. Our empirical results confirm that anomaly detection constrained via AFRs improves upon unconstrained anomaly detection. Specifically, we show that, when equipped with an estimated AFR, an efficient algorithm based on random guessing becomes a strong baseline that several widely-used methods struggle to overcome. On a dataset with a ground-truth AFR available, the current state of the art is outperformed.

Value Identification in Multistakeholder Recommender Systems for Humanities and Historical Research: The Case of the Digital Archive Monasterium.net

Recommender systems remain underutilized in humanities and historical research, despite their potential to enhance the discovery of cultural records. This paper offers an initial value identification of the multiple stakeholders that might be impacted by recommendations in Monasterium.net, a digital archive for historical legal documents. Specifically, we discuss the diverse values and objectives of its stakeholders, such as editors, aggregators, platform owners, researchers, publishers, and funding agencies. These in-depth insights into the potentially conflicting values of stakeholder groups allow designing and adapting recommender systems to enhance their usefulness for humanities and historical research. Additionally, our findings will support deeper engagement with additional stakeholders to refine value models and evaluation metrics for recommender systems in the given domains. Our conclusions are embedded in and applicable to other digital archives and a broader cultural heritage context.

Approximating Families of Sharp Solutions to Fisher's Equation with Physics-Informed Neural Networks

This paper employs physics-informed neural networks (PINNs) to solve Fisher's equation, a fundamental representation of a reaction-diffusion system with both simplicity and significance. The focus lies specifically in investigating Fisher's equation under conditions of large reaction rate coefficients, wherein solutions manifest as traveling waves, posing a challenge for numerical methods due to the occurring steepness of the wave front. To address optimization challenges associated with the standard PINN approach, a residual weighting scheme is introduced. This scheme is designed to enhance the tracking of propagating wave fronts by considering the reaction term in the reaction-diffusion equation. Furthermore, a specific network architecture is studied which is tailored for solutions in the form of traveling waves. Lastly, the capacity of PINNs to approximate an entire family of solutions is assessed by incorporating the reaction rate coefficient as an additional input to the network architecture. This modification enables the approximation of the solution across a broad and continuous range of reaction rate coefficients, thus solving a class of reaction-diffusion systems using a single PINN instance.

Bringing Chemistry to Scale: Loss Weight Adjustment for Multivariate Regression in Deep Learning of Thermochemical Processes

Flamelet models are widely used in computational fluid dynamics to simulate thermochemical processes in turbulent combustion. These models typically employ memory-expensive lookup tables that are predetermined and represent the combustion process to be simulated. Artificial neural networks (ANNs) offer a deep learning approach that can store this tabular data using a small number of network weights, potentially reducing the memory demands of complex simulations by orders of magnitude. However, ANNs with standard training losses often struggle with underrepresented targets in multivariate regression tasks, e.g., when learning minor species mass fractions as part of lookup tables. This paper seeks to improve the accuracy of an ANN when learning multiple species mass fractions of a hydrogen (\ce{H2}) combustion lookup table. We assess a simple, yet effective loss weight adjustment that outperforms the standard mean-squared error optimization and enables accurate learning of all species mass fractions, even of minor species where the standard optimization completely fails. Furthermore, we find that the loss weight adjustment leads to more balanced gradients in the network training, which explains its effectiveness.

Finding the Optimum Design of Large Gas Engines Prechambers Using CFD and Bayesian Optimization

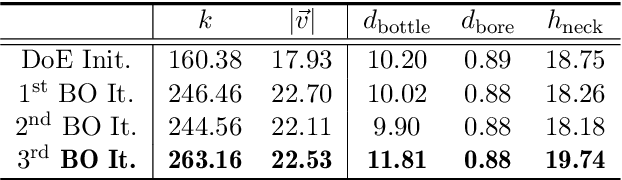
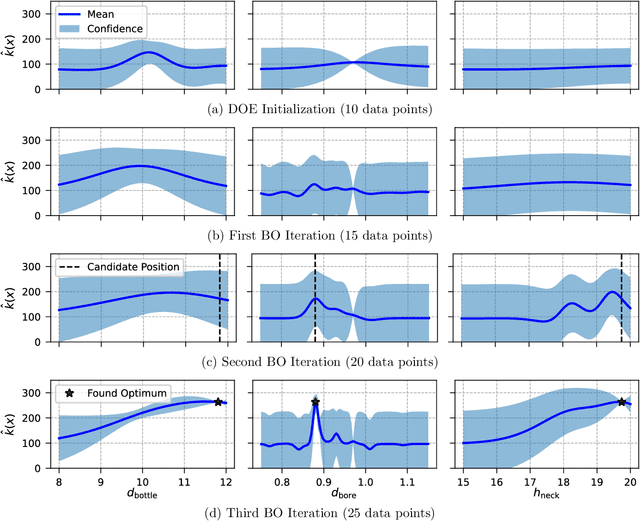
The turbulent jet ignition concept using prechambers is a promising solution to achieve stable combustion at lean conditions in large gas engines, leading to high efficiency at low emission levels. Due to the wide range of design and operating parameters for large gas engine prechambers, the preferred method for evaluating different designs is computational fluid dynamics (CFD), as testing in test bed measurement campaigns is time-consuming and expensive. However, the significant computational time required for detailed CFD simulations due to the complexity of solving the underlying physics also limits its applicability. In optimization settings similar to the present case, i.e., where the evaluation of the objective function(s) is computationally costly, Bayesian optimization has largely replaced classical design-of-experiment. Thus, the present study deals with the computationally efficient Bayesian optimization of large gas engine prechambers design using CFD simulation. Reynolds-averaged-Navier-Stokes simulations are used to determine the target values as a function of the selected prechamber design parameters. The results indicate that the chosen strategy is effective to find a prechamber design that achieves the desired target values.

Cluster Purging: Efficient Outlier Detection based on Rate-Distortion Theory

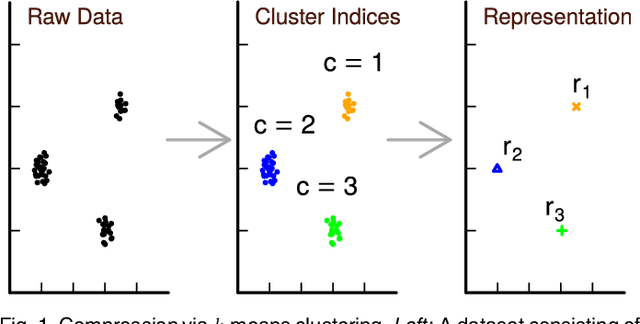
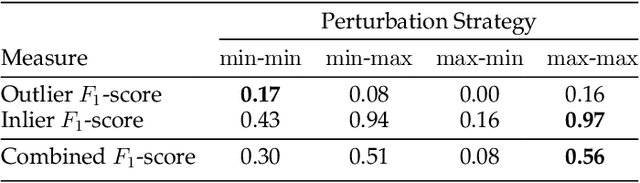
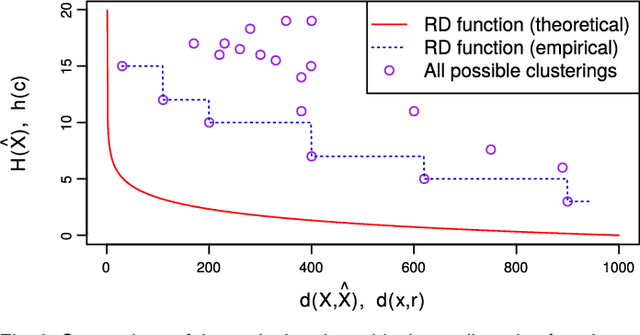
Rate-distortion theory-based outlier detection builds upon the rationale that a good data compression will encode outliers with unique symbols. Based on this rationale, we propose Cluster Purging, which is an extension of clustering-based outlier detection. This extension allows one to assess the representivity of clusterings, and to find data that are best represented by individual unique clusters. We propose two efficient algorithms for performing Cluster Purging, one being parameter-free, while the other algorithm has a parameter that controls representivity estimations, allowing it to be tuned in supervised setups. In an experimental evaluation, we show that Cluster Purging improves upon outliers detected from raw clusterings, and that Cluster Purging competes strongly against state-of-the-art alternatives.

Robust Bayesian Target Value Optimization

We consider the problem of finding an input to a stochastic black box function such that the scalar output of the black box function is as close as possible to a target value in the sense of the expected squared error. While the optimization of stochastic black boxes is classic in (robust) Bayesian optimization, the current approaches based on Gaussian processes predominantly focus either on i) maximization/minimization rather than target value optimization or ii) on the expectation, but not the variance of the output, ignoring output variations due to stochasticity in uncontrollable environmental variables. In this work, we fill this gap and derive acquisition functions for common criteria such as the expected improvement, the probability of improvement, and the lower confidence bound, assuming that aleatoric effects are Gaussian with known variance. Our experiments illustrate that this setting is compatible with certain extensions of Gaussian processes, and show that the thus derived acquisition functions can outperform classical Bayesian optimization even if the latter assumptions are violated. An industrial use case in billet forging is presented.

FUNCK: Information Funnels and Bottlenecks for Invariant Representation Learning

Learning invariant representations that remain useful for a downstream task is still a key challenge in machine learning. We investigate a set of related information funnels and bottleneck problems that claim to learn invariant representations from the data. We also propose a new element to this family of information-theoretic objectives: The Conditional Privacy Funnel with Side Information, which we investigate in fully and semi-supervised settings. Given the generally intractable objectives, we derive tractable approximations using amortized variational inference parameterized by neural networks and study the intrinsic trade-offs of these objectives. We describe empirically the proposed approach and show that with a few labels it is possible to learn fair classifiers and generate useful representations approximately invariant to unwanted sources of variation. Furthermore, we provide insights about the applicability of these methods in real-world scenarios with ordinary tabular datasets when the data is scarce.