Approximating Families of Sharp Solutions to Fisher's Equation with Physics-Informed Neural Networks

This paper employs physics-informed neural networks (PINNs) to solve Fisher's equation, a fundamental representation of a reaction-diffusion system with both simplicity and significance. The focus lies specifically in investigating Fisher's equation under conditions of large reaction rate coefficients, wherein solutions manifest as traveling waves, posing a challenge for numerical methods due to the occurring steepness of the wave front. To address optimization challenges associated with the standard PINN approach, a residual weighting scheme is introduced. This scheme is designed to enhance the tracking of propagating wave fronts by considering the reaction term in the reaction-diffusion equation. Furthermore, a specific network architecture is studied which is tailored for solutions in the form of traveling waves. Lastly, the capacity of PINNs to approximate an entire family of solutions is assessed by incorporating the reaction rate coefficient as an additional input to the network architecture. This modification enables the approximation of the solution across a broad and continuous range of reaction rate coefficients, thus solving a class of reaction-diffusion systems using a single PINN instance.

"UWBCarGraz" Dataset for Car Occupancy Detection using Ultra-Wideband Radar

We present a data-driven car occupancy detection algorithm using ultra-wideband radar based on the ResNet architecture. The algorithm is trained on a dataset of channel impulse responses obtained from measurements at three different activity levels of the occupants (i.e. breathing, talking, moving). We compare the presented algorithm against a state-of-the-art car occupancy detection algorithm based on variational message passing (VMP). Our presented ResNet architecture is able to outperform the VMP algorithm in terms of the area under the receiver operating curve (AUC) at low signal-to-noise ratios (SNRs) for all three activity levels of the target. Specifically, for an SNR of -20 dB the VMP detector achieves an AUC of 0.87 while the ResNet architecture achieves an AUC of 0.91 if the target is sitting still and breathing naturally. The difference in performance for the other activities is similar. To facilitate the implementation in the onboard computer of a car we perform an ablation study to optimize the tradeoff between performance and computational complexity for several ResNet architectures. The dataset used to train and evaluate the algorithm is openly accessible. This facilitates an easy comparison in future works.

Bringing Chemistry to Scale: Loss Weight Adjustment for Multivariate Regression in Deep Learning of Thermochemical Processes

Flamelet models are widely used in computational fluid dynamics to simulate thermochemical processes in turbulent combustion. These models typically employ memory-expensive lookup tables that are predetermined and represent the combustion process to be simulated. Artificial neural networks (ANNs) offer a deep learning approach that can store this tabular data using a small number of network weights, potentially reducing the memory demands of complex simulations by orders of magnitude. However, ANNs with standard training losses often struggle with underrepresented targets in multivariate regression tasks, e.g., when learning minor species mass fractions as part of lookup tables. This paper seeks to improve the accuracy of an ANN when learning multiple species mass fractions of a hydrogen (\ce{H2}) combustion lookup table. We assess a simple, yet effective loss weight adjustment that outperforms the standard mean-squared error optimization and enables accurate learning of all species mass fractions, even of minor species where the standard optimization completely fails. Furthermore, we find that the loss weight adjustment leads to more balanced gradients in the network training, which explains its effectiveness.

Finding the Optimum Design of Large Gas Engines Prechambers Using CFD and Bayesian Optimization

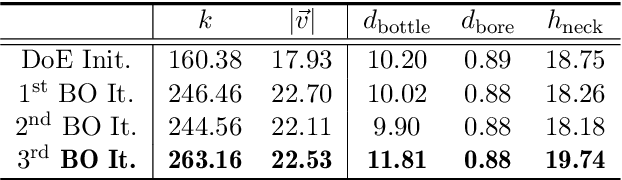
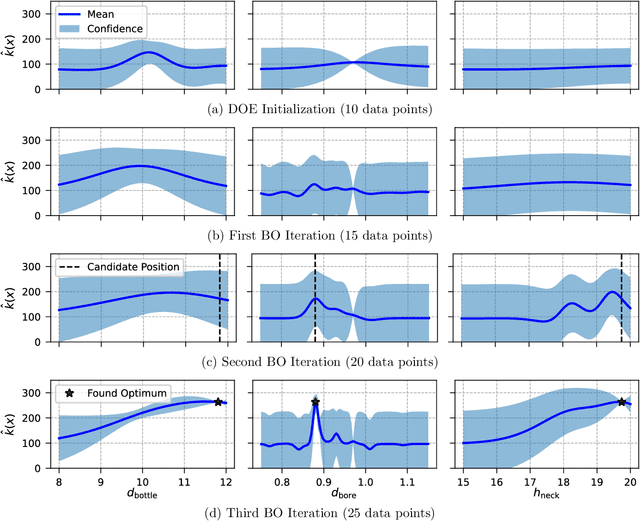
The turbulent jet ignition concept using prechambers is a promising solution to achieve stable combustion at lean conditions in large gas engines, leading to high efficiency at low emission levels. Due to the wide range of design and operating parameters for large gas engine prechambers, the preferred method for evaluating different designs is computational fluid dynamics (CFD), as testing in test bed measurement campaigns is time-consuming and expensive. However, the significant computational time required for detailed CFD simulations due to the complexity of solving the underlying physics also limits its applicability. In optimization settings similar to the present case, i.e., where the evaluation of the objective function(s) is computationally costly, Bayesian optimization has largely replaced classical design-of-experiment. Thus, the present study deals with the computationally efficient Bayesian optimization of large gas engine prechambers design using CFD simulation. Reynolds-averaged-Navier-Stokes simulations are used to determine the target values as a function of the selected prechamber design parameters. The results indicate that the chosen strategy is effective to find a prechamber design that achieves the desired target values.

Understanding the Difficulty of Training Physics-Informed Neural Networks on Dynamical Systems

Physics-informed neural networks (PINNs) seamlessly integrate data and physical constraints into the solving of problems governed by differential equations. In settings with little labeled training data, their optimization relies on the complexity of the embedded physics loss function. Two fundamental questions arise in any discussion of frequently reported convergence issues in PINNs: Why does the optimization often converge to solutions that lack physical behavior? And why do reduced domain methods improve convergence behavior in PINNs? We answer these questions by studying the physics loss function in the vicinity of fixed points of dynamical systems. Experiments on a simple dynamical system demonstrate that physics loss residuals are trivially minimized in the vicinity of fixed points. As a result we observe that solutions corresponding to nonphysical system dynamics can be dominant in the physics loss landscape and optimization. We find that reducing the computational domain lowers the optimization complexity and chance of getting trapped with nonphysical solutions.

Knock Detection in Combustion Engine Time Series Using a Theory-Guided 1D Convolutional Neural Network Approach

This paper introduces a method for the detection of knock occurrences in an internal combustion engine (ICE) using a 1D convolutional neural network trained on in-cylinder pressure data. The model architecture was based on considerations regarding the expected frequency characteristics of knocking combustion. To aid the feature extraction, all cycles were reduced to 60{\deg} CA long windows, with no further processing applied to the pressure traces. The neural networks were trained exclusively on in-cylinder pressure traces from multiple conditions and labels provided by human experts. The best-performing model architecture achieves an accuracy of above 92% on all test sets in a tenfold cross-validation when distinguishing between knocking and non-knocking cycles. In a multi-class problem where each cycle was labeled by the number of experts who rated it as knocking, 78% of cycles were labeled perfectly, while 90% of cycles were classified at most one class from ground truth. They thus considerably outperform the broadly applied MAPO (Maximum Amplitude of Pressure Oscillation) detection method, as well as other references reconstructed from previous works. Our analysis indicates that the neural network learned physically meaningful features connected to engine-characteristic resonance frequencies, thus verifying the intended theory-guided data science approach. Deeper performance investigation further shows remarkable generalization ability to unseen operating points. In addition, the model proved to classify knocking cycles in unseen engines with increased accuracy of 89% after adapting to their features via training on a small number of exclusively non-knocking cycles. The algorithm takes below 1 ms (on CPU) to classify individual cycles, effectively making it suitable for real-time engine control.

On the Pareto Front of Physics-Informed Neural Networks

Recently a new type of deep learning method has emerged, called physics-informed neural networks. Despite their success in solving problems that are governed by partial differential equations, physics-informed neural networks are often difficult to train. Frequently reported convergence issues are still poorly understood and complicate the inference of correct system dynamics. In this paper, we shed light on the training process of physics-informed neural networks. By trading between data- and physics-based constraints in the network training, we study the Pareto front in multi-objective optimization problems. We use the diffusion equation and Navier-Stokes equations in various test environments to analyze the effects of system parameters on the shape of the Pareto front. Additionally, we assess the effectiveness of state-of-the-art adaptive activation functions and adaptive loss weighting methods. Our results demonstrate the prominent role of system parameters in the multi-objective optimization and contribute to understanding convergence properties of physics-informed neural networks.