Approximating Families of Sharp Solutions to Fisher's Equation with Physics-Informed Neural Networks

This paper employs physics-informed neural networks (PINNs) to solve Fisher's equation, a fundamental representation of a reaction-diffusion system with both simplicity and significance. The focus lies specifically in investigating Fisher's equation under conditions of large reaction rate coefficients, wherein solutions manifest as traveling waves, posing a challenge for numerical methods due to the occurring steepness of the wave front. To address optimization challenges associated with the standard PINN approach, a residual weighting scheme is introduced. This scheme is designed to enhance the tracking of propagating wave fronts by considering the reaction term in the reaction-diffusion equation. Furthermore, a specific network architecture is studied which is tailored for solutions in the form of traveling waves. Lastly, the capacity of PINNs to approximate an entire family of solutions is assessed by incorporating the reaction rate coefficient as an additional input to the network architecture. This modification enables the approximation of the solution across a broad and continuous range of reaction rate coefficients, thus solving a class of reaction-diffusion systems using a single PINN instance.

Bringing Chemistry to Scale: Loss Weight Adjustment for Multivariate Regression in Deep Learning of Thermochemical Processes

Flamelet models are widely used in computational fluid dynamics to simulate thermochemical processes in turbulent combustion. These models typically employ memory-expensive lookup tables that are predetermined and represent the combustion process to be simulated. Artificial neural networks (ANNs) offer a deep learning approach that can store this tabular data using a small number of network weights, potentially reducing the memory demands of complex simulations by orders of magnitude. However, ANNs with standard training losses often struggle with underrepresented targets in multivariate regression tasks, e.g., when learning minor species mass fractions as part of lookup tables. This paper seeks to improve the accuracy of an ANN when learning multiple species mass fractions of a hydrogen (\ce{H2}) combustion lookup table. We assess a simple, yet effective loss weight adjustment that outperforms the standard mean-squared error optimization and enables accurate learning of all species mass fractions, even of minor species where the standard optimization completely fails. Furthermore, we find that the loss weight adjustment leads to more balanced gradients in the network training, which explains its effectiveness.

Understanding the Difficulty of Training Physics-Informed Neural Networks on Dynamical Systems

Physics-informed neural networks (PINNs) seamlessly integrate data and physical constraints into the solving of problems governed by differential equations. In settings with little labeled training data, their optimization relies on the complexity of the embedded physics loss function. Two fundamental questions arise in any discussion of frequently reported convergence issues in PINNs: Why does the optimization often converge to solutions that lack physical behavior? And why do reduced domain methods improve convergence behavior in PINNs? We answer these questions by studying the physics loss function in the vicinity of fixed points of dynamical systems. Experiments on a simple dynamical system demonstrate that physics loss residuals are trivially minimized in the vicinity of fixed points. As a result we observe that solutions corresponding to nonphysical system dynamics can be dominant in the physics loss landscape and optimization. We find that reducing the computational domain lowers the optimization complexity and chance of getting trapped with nonphysical solutions.

On the Pareto Front of Physics-Informed Neural Networks

Recently a new type of deep learning method has emerged, called physics-informed neural networks. Despite their success in solving problems that are governed by partial differential equations, physics-informed neural networks are often difficult to train. Frequently reported convergence issues are still poorly understood and complicate the inference of correct system dynamics. In this paper, we shed light on the training process of physics-informed neural networks. By trading between data- and physics-based constraints in the network training, we study the Pareto front in multi-objective optimization problems. We use the diffusion equation and Navier-Stokes equations in various test environments to analyze the effects of system parameters on the shape of the Pareto front. Additionally, we assess the effectiveness of state-of-the-art adaptive activation functions and adaptive loss weighting methods. Our results demonstrate the prominent role of system parameters in the multi-objective optimization and contribute to understanding convergence properties of physics-informed neural networks.

Importance of feature engineering and database selection in a machine learning model: A case study on carbon crystal structures

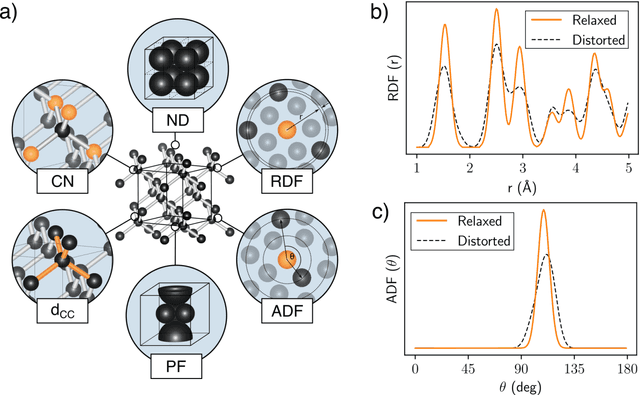
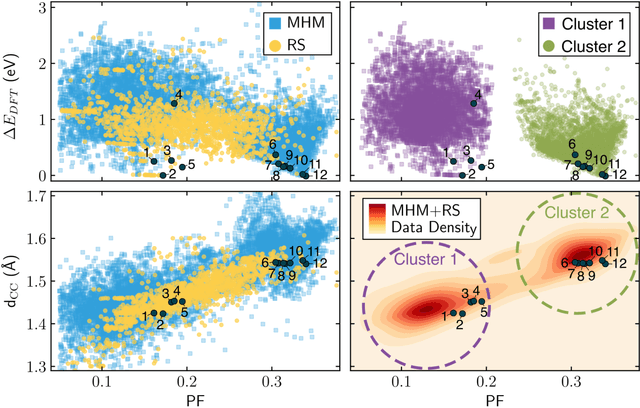
Drive towards improved performance of machine learning models has led to the creation of complex features representing a database of condensed matter systems. The complex features, however, do not offer an intuitive explanation on which physical attributes do improve the performance. The effect of the database on the performance of the trained model is often neglected. In this work we seek to understand in depth the effect that the choice of features and the properties of the database have on a machine learning application. In our experiments, we consider the complex phase space of carbon as a test case, for which we use a set of simple, human understandable and cheaply computable features for the aim of predicting the total energy of the crystal structure. Our study shows that (i) the performance of the machine learning model varies depending on the set of features and the database, (ii) is not transferable to every structure in the phase space and (iii) depends on how well structures are represented in the database.