Stochastic Modeling of Inhomogeneities in the Aortic Wall and Uncertainty Quantification using a Bayesian Encoder-Decoder Surrogate

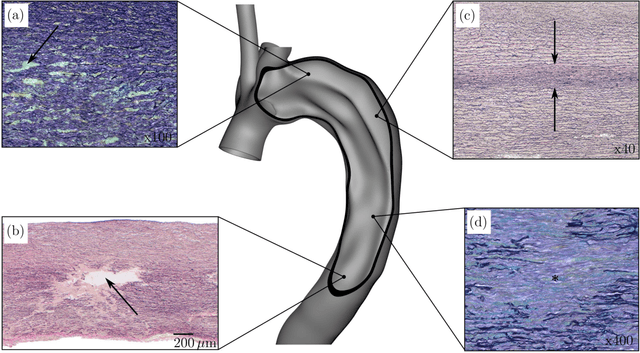
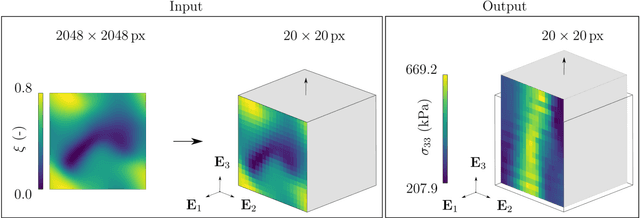
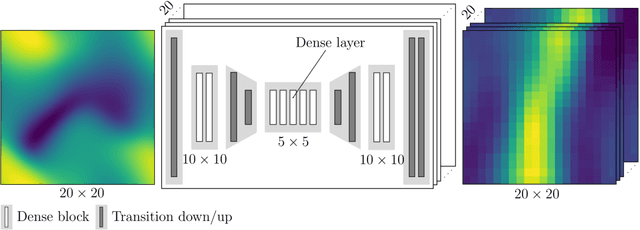
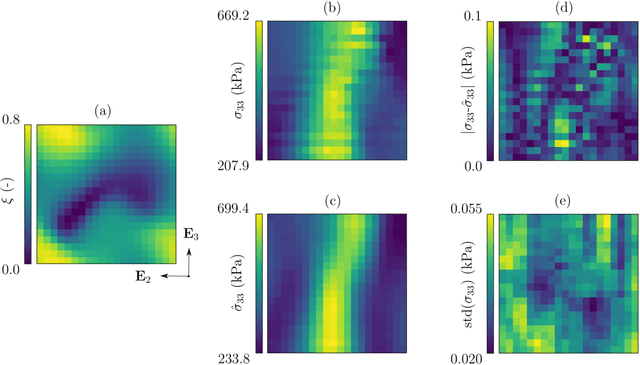
Inhomogeneities in the aortic wall can lead to localized stress accumulations, possibly initiating dissection. In many cases, a dissection results from pathological changes such as fragmentation or loss of elastic fibers. But it has been shown that even the healthy aortic wall has an inherent heterogeneous microstructure. Some parts of the aorta are particularly susceptible to the development of inhomogeneities due to pathological changes, however, the distribution in the aortic wall and the spatial extent, such as size, shape, and type, are difficult to predict. Motivated by this observation, we describe the heterogeneous distribution of elastic fiber degradation in the dissected aortic wall using a stochastic constitutive model. For this purpose, random field realizations, which model the stochastic distribution of degraded elastic fibers, are generated over a non-equidistant grid. The random field then serves as input for a uni-axial extension test of the pathological aortic wall, solved with the finite-element (FE) method. To include the microstructure of the dissected aortic wall, a constitutive model developed in a previous study is applied, which also includes an approach to model the degradation of inter-lamellar elastic fibers. Then to assess the uncertainty in the output stress distribution due to this stochastic constitutive model, a convolutional neural network, specifically a Bayesian encoder-decoder, was used as a surrogate model that maps the random input fields to the output stress distribution obtained from the FE analysis. The results show that the neural network is able to predict the stress distribution of the FE analysis while significantly reducing the computational time. In addition, it provides the probability for exceeding critical stresses within the aortic wall, which could allow for the prediction of delamination or fatal rupture.

Importance of feature engineering and database selection in a machine learning model: A case study on carbon crystal structures

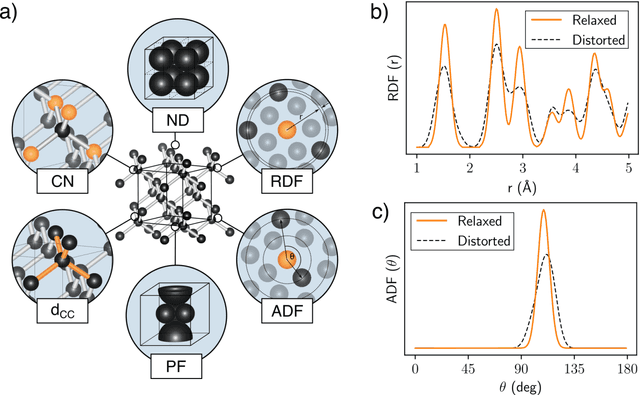
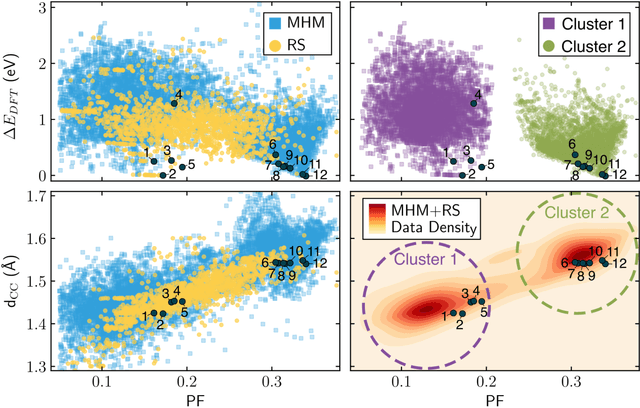
Drive towards improved performance of machine learning models has led to the creation of complex features representing a database of condensed matter systems. The complex features, however, do not offer an intuitive explanation on which physical attributes do improve the performance. The effect of the database on the performance of the trained model is often neglected. In this work we seek to understand in depth the effect that the choice of features and the properties of the database have on a machine learning application. In our experiments, we consider the complex phase space of carbon as a test case, for which we use a set of simple, human understandable and cheaply computable features for the aim of predicting the total energy of the crystal structure. Our study shows that (i) the performance of the machine learning model varies depending on the set of features and the database, (ii) is not transferable to every structure in the phase space and (iii) depends on how well structures are represented in the database.