Temporally resolved aortic 3D shape reconstruction from a limited number of cine 2D MRI slices

Background and Objective: We propose a shape reconstruction framework to generate time-resolved, patient-specific 3D aortic geometries from a limited number of standard cine 2D magnetic resonance imaging (MRI) acquisitions. A statistical shape model of the aorta is coupled with differentiable volumetric mesh optimization to obtain personalized aortic meshes. Methods: The statistical shape model was constructed from retrospective data and optimized 2D slice placements along the aortic arch were identified. Cine 2D MRI slices were then acquired in 30 subjects (19 volunteers, 11 aortic stenosis patients). After manual segmentation, time-resolved aortic models were generated via differentiable volumetric mesh optimization to derive vessel shape features, centerline parameters, and radial wall strain. In 10 subjects, additional 4D flow MRI was acquired to compare peak-systolic shapes. Results: Anatomically accurate aortic geometries were obtained from as few as six cine 2D MRI slices, achieving a mean +/- standard deviation Dice score of (89.9 +/- 1.6) %, Intersection over Union of (81.7 +/- 2.7) %, Hausdorff distance of (7.3 +/- 3.3) mm, and Chamfer distance of (3.7 +/- 0.6) mm relative to 4D flow MRI. The mean absolute radius error was (0.8 +/- 0.6) mm. Significant age-related differences were observed for all shape features, including radial strain, which decreased progressively ((11.00 +/- 3.11) x 10-2 vs. (3.74 +/- 1.25) x 10-2 vs. (2.89 +/- 0.87) x 10-2 for young, mid-age, and elderly groups). Conclusion: The proposed method enables efficient extraction of time-resolved 3D aortic meshes from limited sets of standard cine 2D MRI acquisitions, suitable for computational shape and strain analysis.

Stochastic Modeling of Inhomogeneities in the Aortic Wall and Uncertainty Quantification using a Bayesian Encoder-Decoder Surrogate

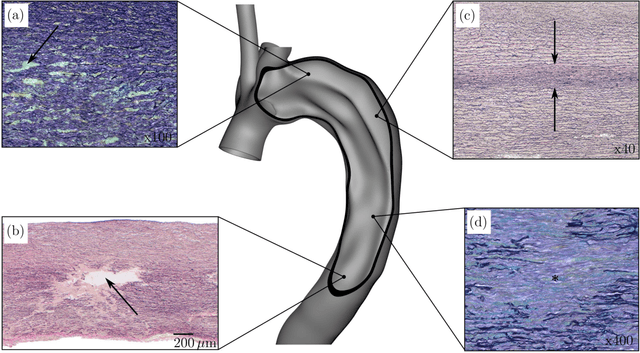
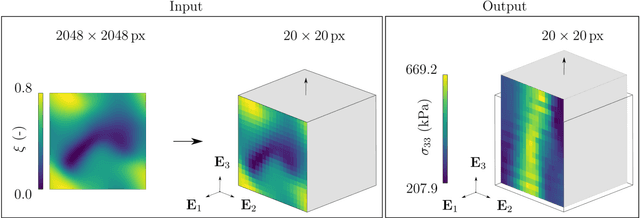
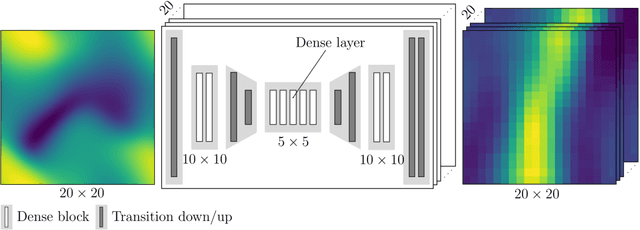
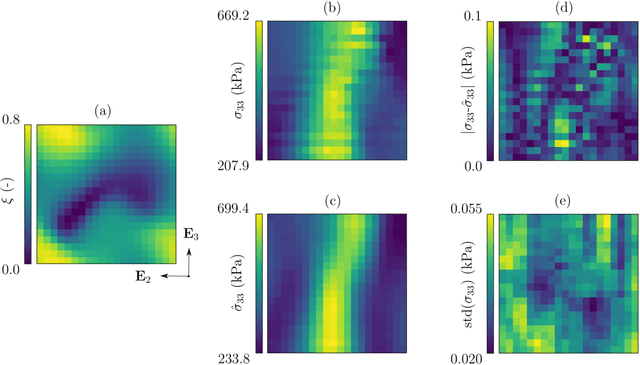
Inhomogeneities in the aortic wall can lead to localized stress accumulations, possibly initiating dissection. In many cases, a dissection results from pathological changes such as fragmentation or loss of elastic fibers. But it has been shown that even the healthy aortic wall has an inherent heterogeneous microstructure. Some parts of the aorta are particularly susceptible to the development of inhomogeneities due to pathological changes, however, the distribution in the aortic wall and the spatial extent, such as size, shape, and type, are difficult to predict. Motivated by this observation, we describe the heterogeneous distribution of elastic fiber degradation in the dissected aortic wall using a stochastic constitutive model. For this purpose, random field realizations, which model the stochastic distribution of degraded elastic fibers, are generated over a non-equidistant grid. The random field then serves as input for a uni-axial extension test of the pathological aortic wall, solved with the finite-element (FE) method. To include the microstructure of the dissected aortic wall, a constitutive model developed in a previous study is applied, which also includes an approach to model the degradation of inter-lamellar elastic fibers. Then to assess the uncertainty in the output stress distribution due to this stochastic constitutive model, a convolutional neural network, specifically a Bayesian encoder-decoder, was used as a surrogate model that maps the random input fields to the output stress distribution obtained from the FE analysis. The results show that the neural network is able to predict the stress distribution of the FE analysis while significantly reducing the computational time. In addition, it provides the probability for exceeding critical stresses within the aortic wall, which could allow for the prediction of delamination or fatal rupture.