Robust Bayesian Target Value Optimization

We consider the problem of finding an input to a stochastic black box function such that the scalar output of the black box function is as close as possible to a target value in the sense of the expected squared error. While the optimization of stochastic black boxes is classic in (robust) Bayesian optimization, the current approaches based on Gaussian processes predominantly focus either on i) maximization/minimization rather than target value optimization or ii) on the expectation, but not the variance of the output, ignoring output variations due to stochasticity in uncontrollable environmental variables. In this work, we fill this gap and derive acquisition functions for common criteria such as the expected improvement, the probability of improvement, and the lower confidence bound, assuming that aleatoric effects are Gaussian with known variance. Our experiments illustrate that this setting is compatible with certain extensions of Gaussian processes, and show that the thus derived acquisition functions can outperform classical Bayesian optimization even if the latter assumptions are violated. An industrial use case in billet forging is presented.

A connection between probability, physics and neural networks

We illustrate an approach that can be exploited for constructing neural networks which a priori obey physical laws. We start with a simple single-layer neural network (NN) but refrain from choosing the activation functions yet. Under certain conditions and in the infinite-width limit, we may apply the central limit theorem, upon which the NN output becomes Gaussian. We may then investigate and manipulate the limit network by falling back on Gaussian process (GP) theory. It is observed that linear operators acting upon a GP again yield a GP. This also holds true for differential operators defining differential equations and describing physical laws. If we demand the GP, or equivalently the limit network, to obey the physical law, then this yields an equation for the covariance function or kernel of the GP, whose solution equivalently constrains the model to obey the physical law. The central limit theorem then suggests that NNs can be constructed to obey a physical law by choosing the activation functions such that they match a particular kernel in the infinite-width limit. The activation functions constructed in this way guarantee the NN to a priori obey the physics, up to the approximation error of non-infinite network width. Simple examples of the homogeneous 1D-Helmholtz equation are discussed and compared to naive kernels and activations.

Stochastic Modeling of Inhomogeneities in the Aortic Wall and Uncertainty Quantification using a Bayesian Encoder-Decoder Surrogate

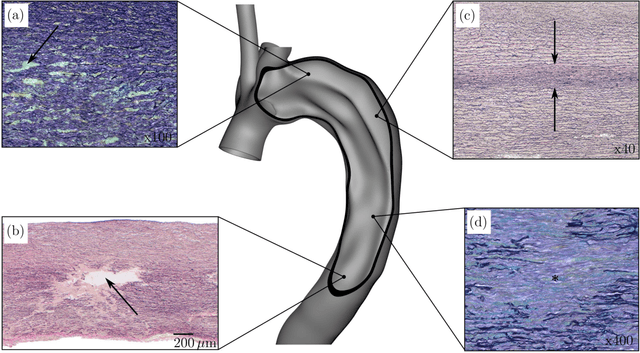
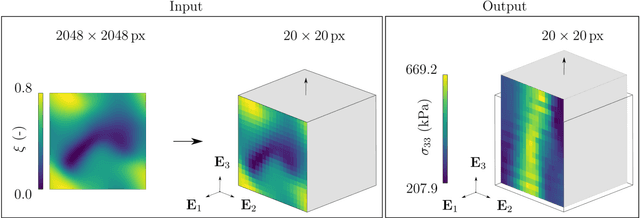
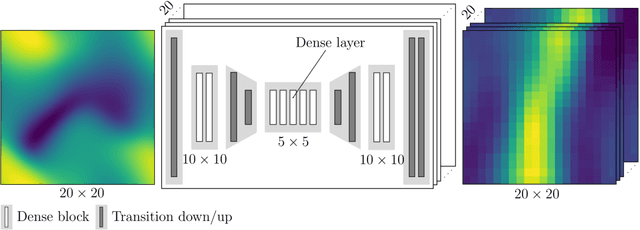
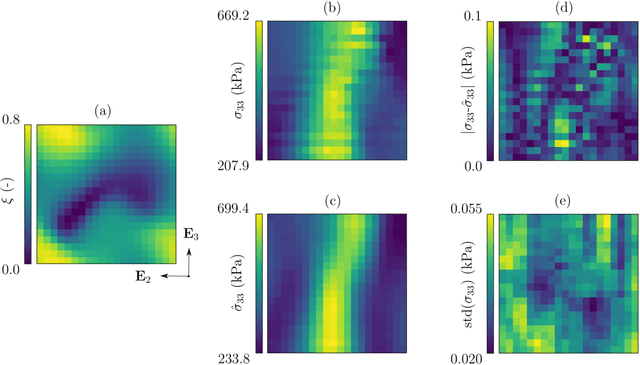
Inhomogeneities in the aortic wall can lead to localized stress accumulations, possibly initiating dissection. In many cases, a dissection results from pathological changes such as fragmentation or loss of elastic fibers. But it has been shown that even the healthy aortic wall has an inherent heterogeneous microstructure. Some parts of the aorta are particularly susceptible to the development of inhomogeneities due to pathological changes, however, the distribution in the aortic wall and the spatial extent, such as size, shape, and type, are difficult to predict. Motivated by this observation, we describe the heterogeneous distribution of elastic fiber degradation in the dissected aortic wall using a stochastic constitutive model. For this purpose, random field realizations, which model the stochastic distribution of degraded elastic fibers, are generated over a non-equidistant grid. The random field then serves as input for a uni-axial extension test of the pathological aortic wall, solved with the finite-element (FE) method. To include the microstructure of the dissected aortic wall, a constitutive model developed in a previous study is applied, which also includes an approach to model the degradation of inter-lamellar elastic fibers. Then to assess the uncertainty in the output stress distribution due to this stochastic constitutive model, a convolutional neural network, specifically a Bayesian encoder-decoder, was used as a surrogate model that maps the random input fields to the output stress distribution obtained from the FE analysis. The results show that the neural network is able to predict the stress distribution of the FE analysis while significantly reducing the computational time. In addition, it provides the probability for exceeding critical stresses within the aortic wall, which could allow for the prediction of delamination or fatal rupture.