Establishing and Evaluating Trustworthy AI: Overview and Research Challenges

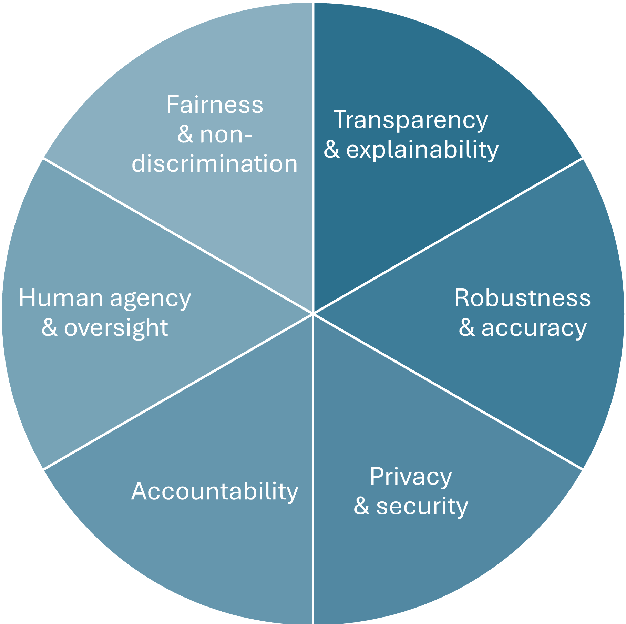
Artificial intelligence (AI) technologies (re-)shape modern life, driving innovation in a wide range of sectors. However, some AI systems have yielded unexpected or undesirable outcomes or have been used in questionable manners. As a result, there has been a surge in public and academic discussions about aspects that AI systems must fulfill to be considered trustworthy. In this paper, we synthesize existing conceptualizations of trustworthy AI along six requirements: 1) human agency and oversight, 2) fairness and non-discrimination, 3) transparency and explainability, 4) robustness and accuracy, 5) privacy and security, and 6) accountability. For each one, we provide a definition, describe how it can be established and evaluated, and discuss requirement-specific research challenges. Finally, we conclude this analysis by identifying overarching research challenges across the requirements with respect to 1) interdisciplinary research, 2) conceptual clarity, 3) context-dependency, 4) dynamics in evolving systems, and 5) investigations in real-world contexts. Thus, this paper synthesizes and consolidates a wide-ranging and active discussion currently taking place in various academic sub-communities and public forums. It aims to serve as a reference for a broad audience and as a basis for future research directions.

Constraining Anomaly Detection with Anomaly-Free Regions

We propose the novel concept of anomaly-free regions (AFR) to improve anomaly detection. An AFR is a region in the data space for which it is known that there are no anomalies inside it, e.g., via domain knowledge. This region can contain any number of normal data points and can be anywhere in the data space. AFRs have the key advantage that they constrain the estimation of the distribution of non-anomalies: The estimated probability mass inside the AFR must be consistent with the number of normal data points inside the AFR. Based on this insight, we provide a solid theoretical foundation and a reference implementation of anomaly detection using AFRs. Our empirical results confirm that anomaly detection constrained via AFRs improves upon unconstrained anomaly detection. Specifically, we show that, when equipped with an estimated AFR, an efficient algorithm based on random guessing becomes a strong baseline that several widely-used methods struggle to overcome. On a dataset with a ground-truth AFR available, the current state of the art is outperformed.

Activation Bottleneck: Sigmoidal Neural Networks Cannot Forecast a Straight Line

A neural network has an activation bottleneck if one of its hidden layers has a bounded image. We show that networks with an activation bottleneck cannot forecast unbounded sequences such as straight lines, random walks, or any sequence with a trend: The difference between prediction and ground truth becomes arbitrary large, regardless of the training procedure. Widely-used neural network architectures such as LSTM and GRU suffer from this limitation. In our analysis, we characterize activation bottlenecks and explain why they prevent sigmoidal networks from learning unbounded sequences. We experimentally validate our findings and discuss modifications to network architectures which mitigate the effects of activation bottlenecks.

A Formally Robust Time Series Distance Metric

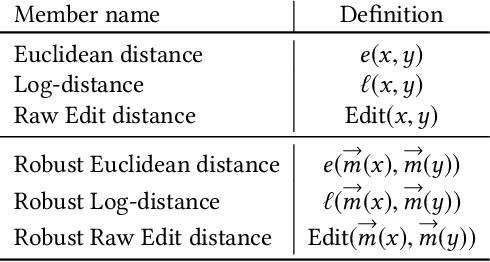
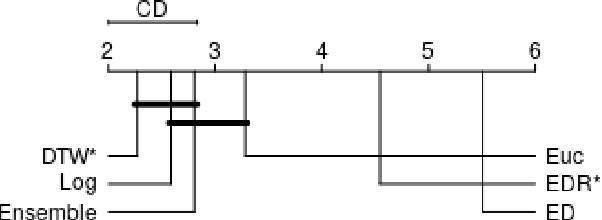
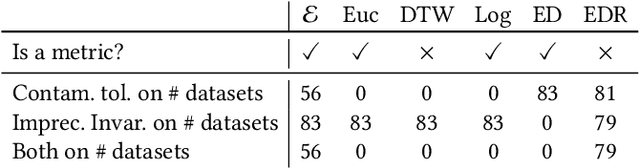
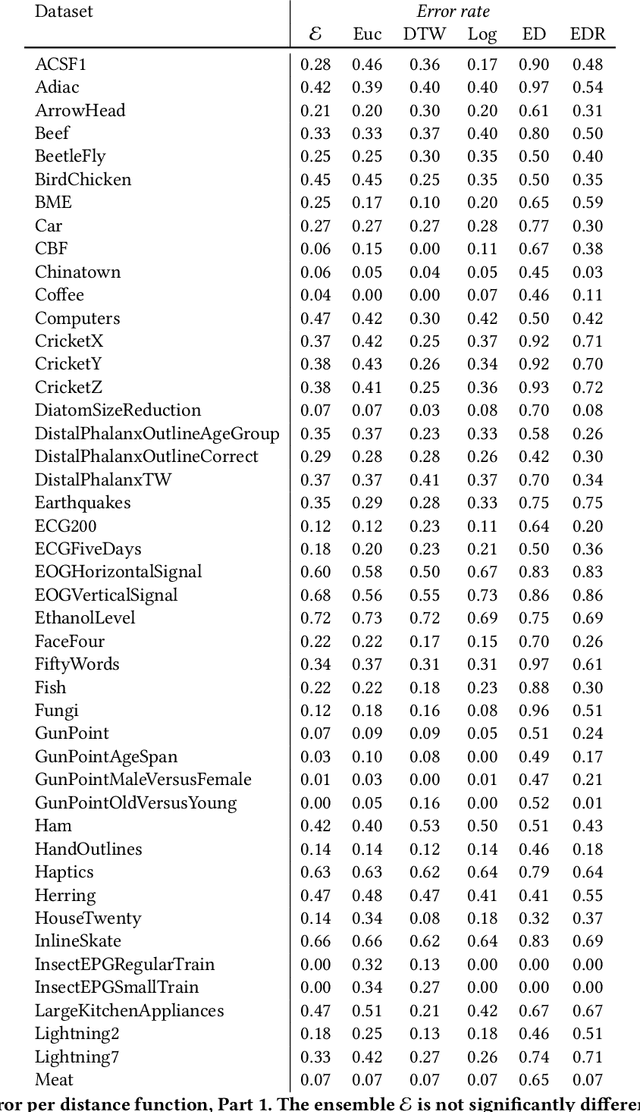
Distance-based classification is among the most competitive classification methods for time series data. The most critical component of distance-based classification is the selected distance function. Past research has proposed various different distance metrics or measures dedicated to particular aspects of real-world time series data, yet there is an important aspect that has not been considered so far: Robustness against arbitrary data contamination. In this work, we propose a novel distance metric that is robust against arbitrarily "bad" contamination and has a worst-case computational complexity of $\mathcal{O}(n\log n)$. We formally argue why our proposed metric is robust, and demonstrate in an empirical evaluation that the metric yields competitive classification accuracy when applied in k-Nearest Neighbor time series classification.

Robust Parameter-Free Season Length Detection in Time Series

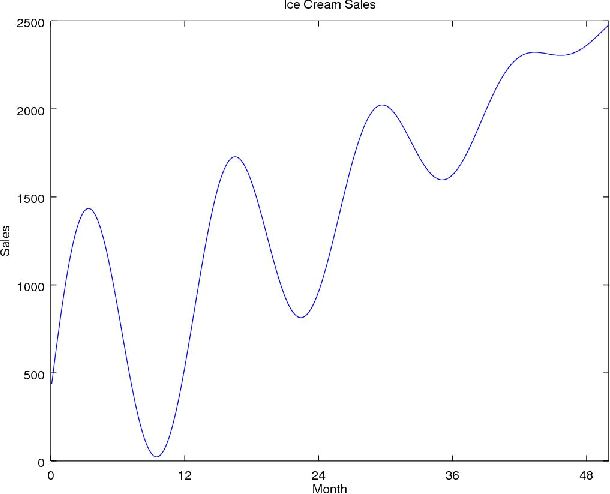
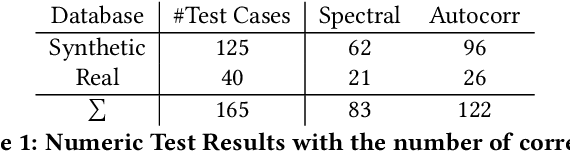
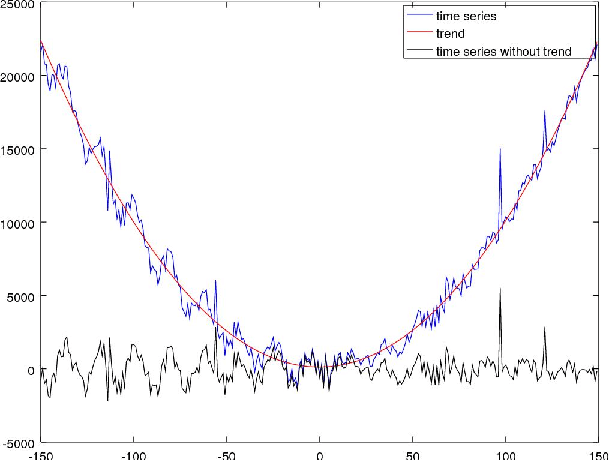
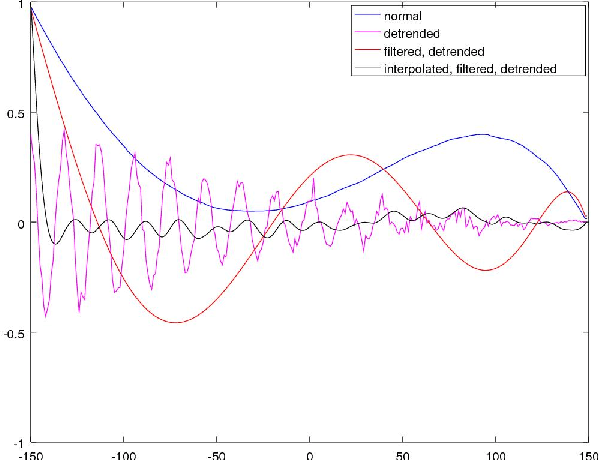
The in-depth analysis of time series has gained a lot of research interest in recent years, with the identification of periodic patterns being one important aspect. Many of the methods for identifying periodic patterns require time series' season length as input parameter. There exist only a few algorithms for automatic season length approximation. Many of these rely on simplifications such as data discretization and user defined parameters. This paper presents an algorithm for season length detection that is designed to be sufficiently reliable to be used in practical applications and does not require any input other than the time series to be analyzed. The algorithm estimates a time series' season length by interpolating, filtering and detrending the data. This is followed by analyzing the distances between zeros in the directly corresponding autocorrelation function. Our algorithm was tested against a comparable algorithm and outperformed it by passing 122 out of 165 tests, while the existing algorithm passed 83 tests. The robustness of our method can be jointly attributed to both the algorithmic approach and also to design decisions taken at the implementational level.