Marek Smieja
Semi-Supervised Clustering via Markov Chain Aggregation
Dec 17, 2021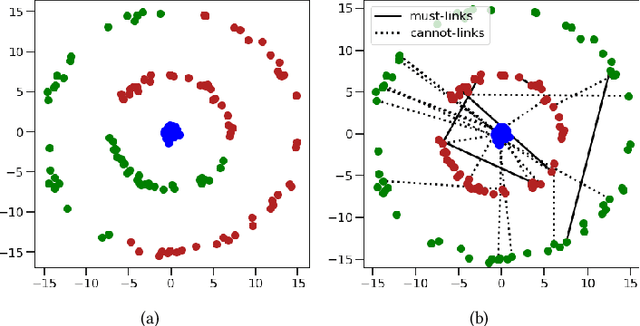
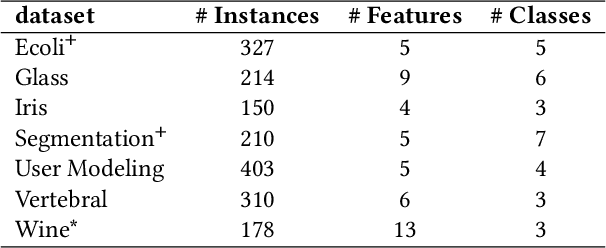
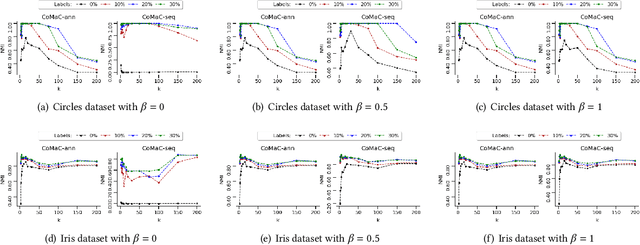
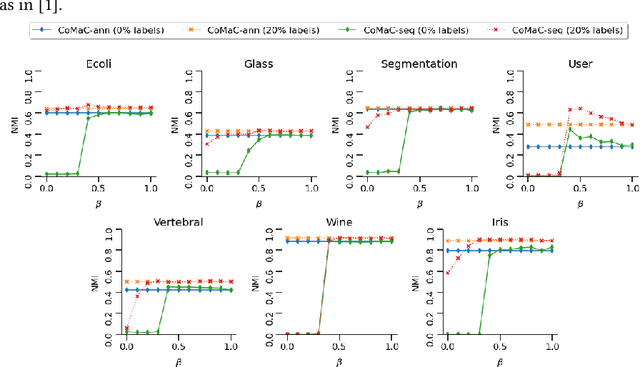
Abstract:We connect the problem of semi-supervised clustering to constrained Markov aggregation, i.e., the task of partitioning the state space of a Markov chain. We achieve this connection by considering every data point in the dataset as an element of the Markov chain's state space, by defining the transition probabilities between states via similarities between corresponding data points, and by incorporating semi-supervision information as hard constraints in a Hartigan-style algorithm. The introduced Constrained Markov Clustering (CoMaC) is an extension of a recent information-theoretic framework for (unsupervised) Markov aggregation to the semi-supervised case. Instantiating CoMaC for certain parameter settings further generalizes two previous information-theoretic objectives for unsupervised clustering. Our results indicate that CoMaC is competitive with the state-of-the-art. Furthermore, our approach is less sensitive to hyperparameter settings than the unsupervised counterpart, which is especially attractive in the semi-supervised setting characterized by little labeled data.
Processing of missing data by neural networks
Sep 12, 2018



Abstract:We propose a general, theoretically justified mechanism for processing missing data by neural networks. Our idea is to replace typical neuron response in the first hidden layer by its expected value. This approach can be applied for various types of networks at minimal cost in their modification. Moreover, in contrast to recent approaches, it does not require complete data for training. Experimental results performed on different types of architectures show that our method gives better results than typical imputation strategies and other methods dedicated for incomplete data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge