Semi-Supervised Clustering via Markov Chain Aggregation
Paper and Code
Dec 17, 2021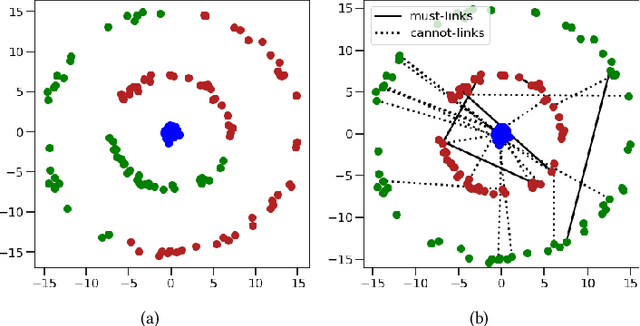
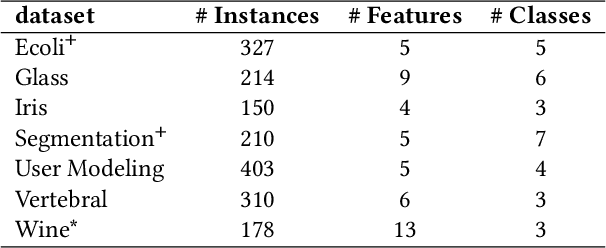
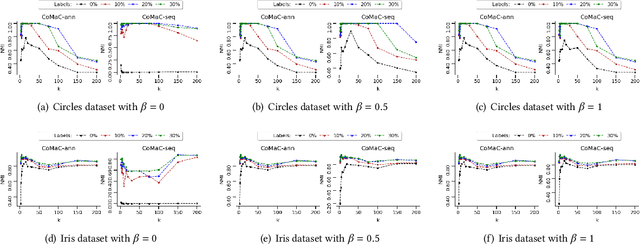
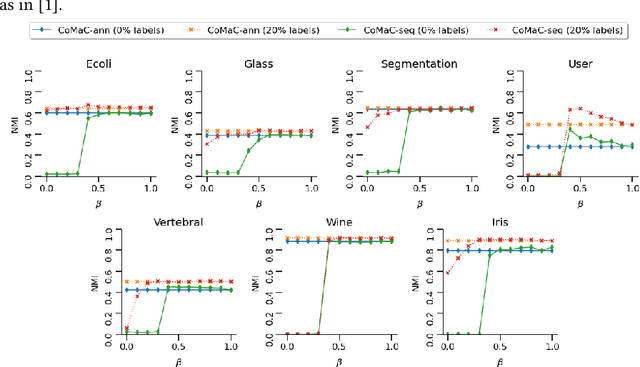
We connect the problem of semi-supervised clustering to constrained Markov aggregation, i.e., the task of partitioning the state space of a Markov chain. We achieve this connection by considering every data point in the dataset as an element of the Markov chain's state space, by defining the transition probabilities between states via similarities between corresponding data points, and by incorporating semi-supervision information as hard constraints in a Hartigan-style algorithm. The introduced Constrained Markov Clustering (CoMaC) is an extension of a recent information-theoretic framework for (unsupervised) Markov aggregation to the semi-supervised case. Instantiating CoMaC for certain parameter settings further generalizes two previous information-theoretic objectives for unsupervised clustering. Our results indicate that CoMaC is competitive with the state-of-the-art. Furthermore, our approach is less sensitive to hyperparameter settings than the unsupervised counterpart, which is especially attractive in the semi-supervised setting characterized by little labeled data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge