Christian Toth
Rao-Blackwellising Bayesian Causal Inference
Feb 22, 2024Abstract:Bayesian causal inference, i.e., inferring a posterior over causal models for the use in downstream causal reasoning tasks, poses a hard computational inference problem that is little explored in literature. In this work, we combine techniques from order-based MCMC structure learning with recent advances in gradient-based graph learning into an effective Bayesian causal inference framework. Specifically, we decompose the problem of inferring the causal structure into (i) inferring a topological order over variables and (ii) inferring the parent sets for each variable. When limiting the number of parents per variable, we can exactly marginalise over the parent sets in polynomial time. We further use Gaussian processes to model the unknown causal mechanisms, which also allows their exact marginalisation. This introduces a Rao-Blackwellization scheme, where all components are eliminated from the model, except for the causal order, for which we learn a distribution via gradient-based optimisation. The combination of Rao-Blackwellization with our sequential inference procedure for causal orders yields state-of-the-art on linear and non-linear additive noise benchmarks with scale-free and Erdos-Renyi graph structures.
Active Bayesian Causal Inference
Jun 04, 2022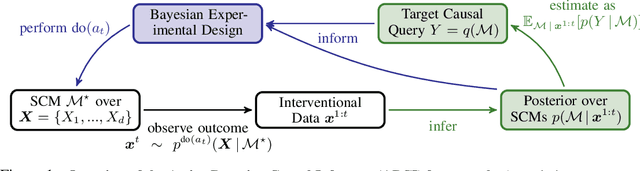

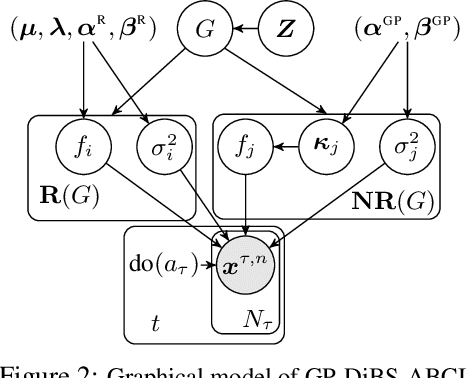
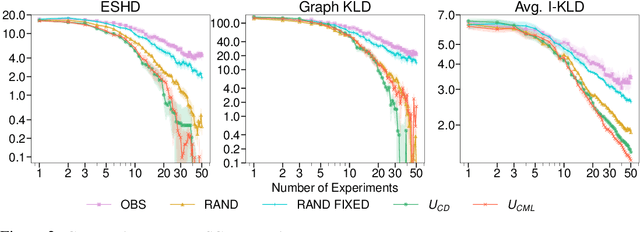
Abstract:Causal discovery and causal reasoning are classically treated as separate and consecutive tasks: one first infers the causal graph, and then uses it to estimate causal effects of interventions. However, such a two-stage approach is uneconomical, especially in terms of actively collected interventional data, since the causal query of interest may not require a fully-specified causal model. From a Bayesian perspective, it is also unnatural, since a causal query (e.g., the causal graph or some causal effect) can be viewed as a latent quantity subject to posterior inference -- other unobserved quantities that are not of direct interest (e.g., the full causal model) ought to be marginalized out in this process and contribute to our epistemic uncertainty. In this work, we propose Active Bayesian Causal Inference (ABCI), a fully-Bayesian active learning framework for integrated causal discovery and reasoning, which jointly infers a posterior over causal models and queries of interest. In our approach to ABCI, we focus on the class of causally-sufficient, nonlinear additive noise models, which we model using Gaussian processes. We sequentially design experiments that are maximally informative about our target causal query, collect the corresponding interventional data, and update our beliefs to choose the next experiment. Through simulations, we demonstrate that our approach is more data-efficient than several baselines that only focus on learning the full causal graph. This allows us to accurately learn downstream causal queries from fewer samples while providing well-calibrated uncertainty estimates for the quantities of interest.
Synwalk -- Community Detection via Random Walk Modelling
Jan 21, 2021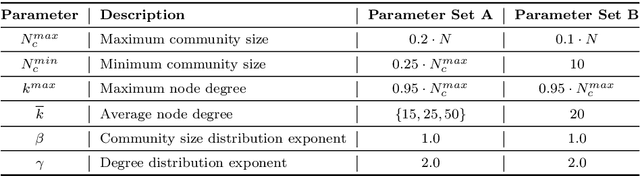



Abstract:Complex systems, abstractly represented as networks, are ubiquitous in everyday life. Analyzing and understanding these systems requires, among others, tools for community detection. As no single best community detection algorithm can exist, robustness across a wide variety of problem settings is desirable. In this work, we present Synwalk, a random walk-based community detection method. Synwalk builds upon a solid theoretical basis and detects communities by synthesizing the random walk induced by the given network from a class of candidate random walks. We thoroughly validate the effectiveness of our approach on synthetic and empirical networks, respectively, and compare Synwalk's performance with the performance of Infomap and Walktrap. Our results indicate that Synwalk performs robustly on networks with varying mixing parameters and degree distributions. We outperform Infomap on networks with high mixing parameter, and Infomap and Walktrap on networks with many small communities and low average degree. Our work has a potential to inspire further development of community detection via synthesis of random walks and we provide concrete ideas for future research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge