Self-attention for Enhanced OAMP Detection in MIMO Systems

Multiple-Input Multiple-Output (MIMO) systems are essential for wireless communications. Sinceclassical algorithms for symbol detection in MIMO setups require large computational resourcesor provide poor results, data-driven algorithms are becoming more popular. Most of the proposedalgorithms, however, introduce approximations leading to degraded performance for realistic MIMOsystems. In this paper, we introduce a neural-enhanced hybrid model, augmenting the analyticbackbone algorithm with state-of-the-art neural network components. In particular, we introduce aself-attention model for the enhancement of the iterative Orthogonal Approximate Message Passing(OAMP)-based decoding algorithm. In our experiments, we show that the proposed model canoutperform existing data-driven approaches for OAMP while having improved generalization to otherSNR values at limited computational overhead.

Graph Neural Networks for Massive MIMO Detection

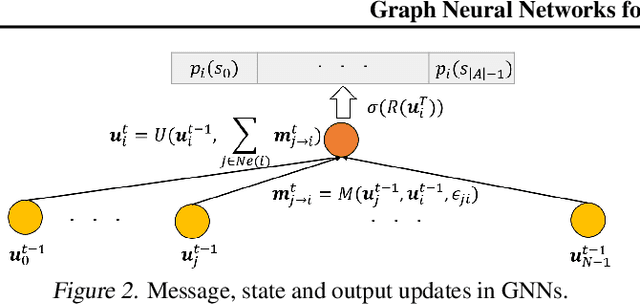
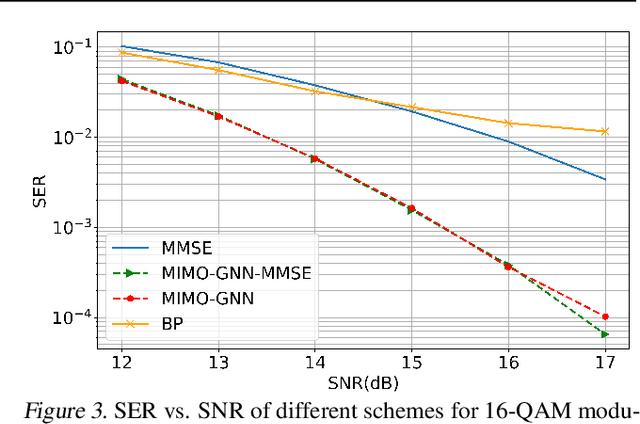
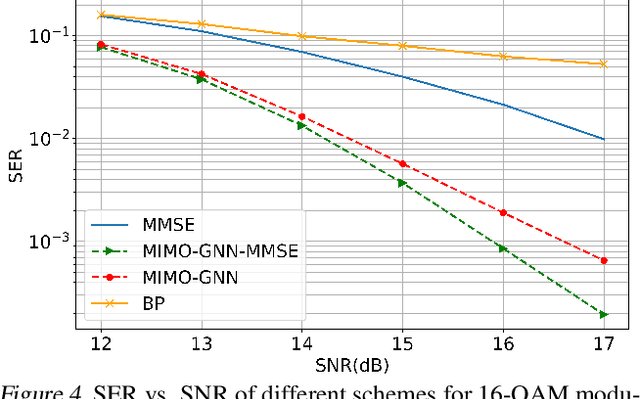
In this paper, we innovately use graph neural networks (GNNs) to learn a message-passing solution for the inference task of massive multiple multiple-input multiple-output (MIMO) detection in wireless communication. We adopt a graphical model based on the Markov random field (MRF) where belief propagation (BP) yields poor results when it assumes a uniform prior over the transmitted symbols. Numerical simulations show that, under the uniform prior assumption, our GNN-based MIMO detection solution outperforms the minimum mean-squared error (MMSE) baseline detector, in contrast to BP. Furthermore, experiments demonstrate that the performance of the algorithm slightly improves by incorporating MMSE information into the prior.

$α$ Belief Propagation as Fully Factorized Approximation

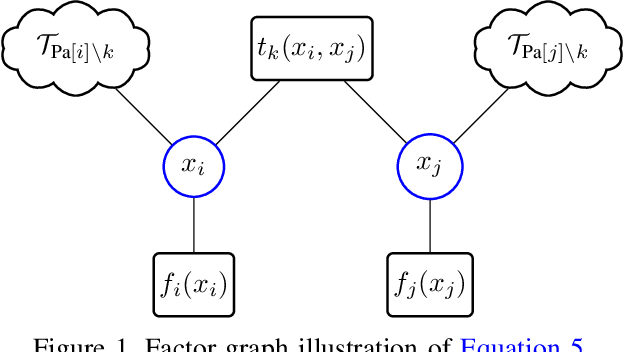
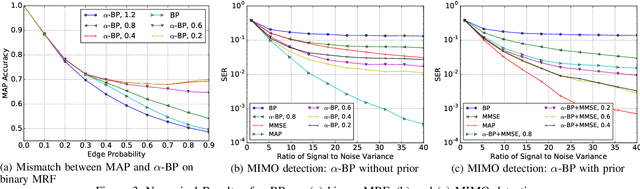
Belief propagation (BP) can do exact inference in loop-free graphs, but its performance could be poor in graphs with loops, and the understanding of its solution is limited. This work gives an interpretable belief propagation rule that is actually minimization of a localized $\alpha$-divergence. We term this algorithm as $\alpha$ belief propagation ($\alpha$-BP). The performance of $\alpha$-BP is tested in MAP (maximum a posterior) inference problems, where $\alpha$-BP can outperform (loopy) BP by a significant margin even in fully-connected graphs.