Jinliang Huang
Graph Neural Networks for Massive MIMO Detection
Jul 11, 2020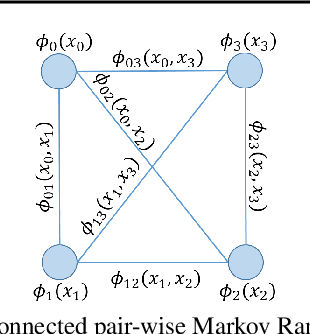
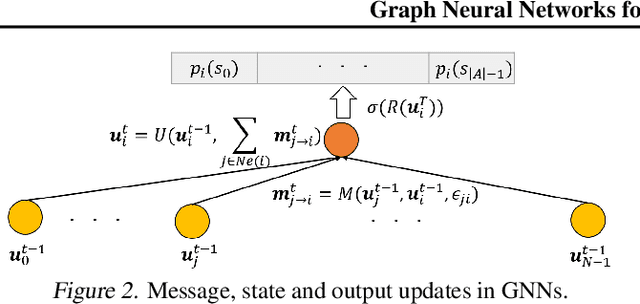
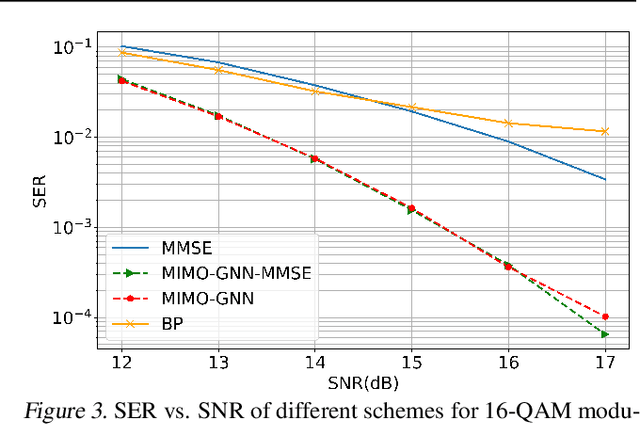
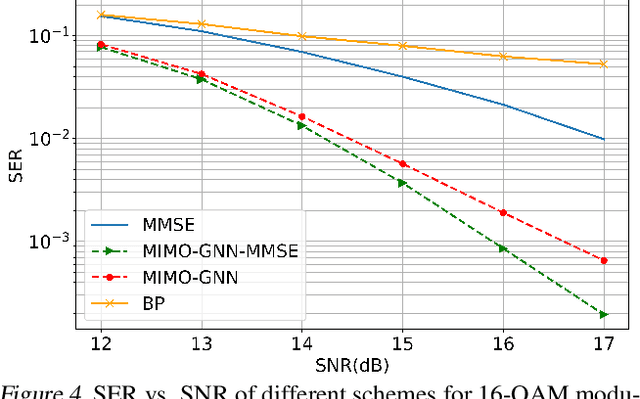
Abstract:In this paper, we innovately use graph neural networks (GNNs) to learn a message-passing solution for the inference task of massive multiple multiple-input multiple-output (MIMO) detection in wireless communication. We adopt a graphical model based on the Markov random field (MRF) where belief propagation (BP) yields poor results when it assumes a uniform prior over the transmitted symbols. Numerical simulations show that, under the uniform prior assumption, our GNN-based MIMO detection solution outperforms the minimum mean-squared error (MMSE) baseline detector, in contrast to BP. Furthermore, experiments demonstrate that the performance of the algorithm slightly improves by incorporating MMSE information into the prior.
$α$ Belief Propagation as Fully Factorized Approximation
Aug 23, 2019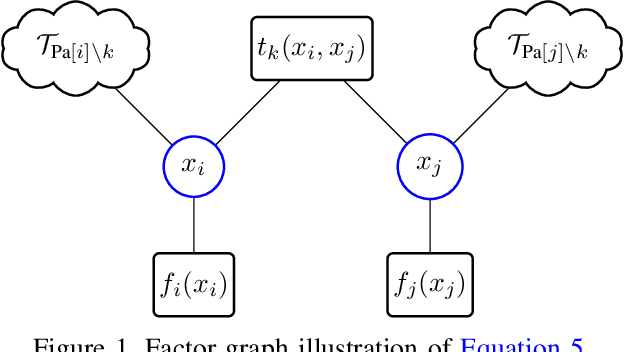
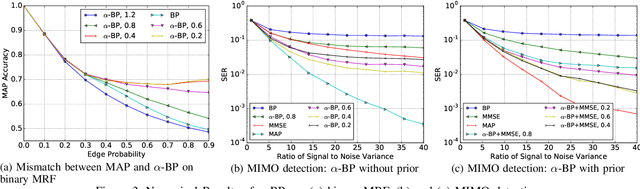
Abstract:Belief propagation (BP) can do exact inference in loop-free graphs, but its performance could be poor in graphs with loops, and the understanding of its solution is limited. This work gives an interpretable belief propagation rule that is actually minimization of a localized $\alpha$-divergence. We term this algorithm as $\alpha$ belief propagation ($\alpha$-BP). The performance of $\alpha$-BP is tested in MAP (maximum a posterior) inference problems, where $\alpha$-BP can outperform (loopy) BP by a significant margin even in fully-connected graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge