$α$ Belief Propagation as Fully Factorized Approximation

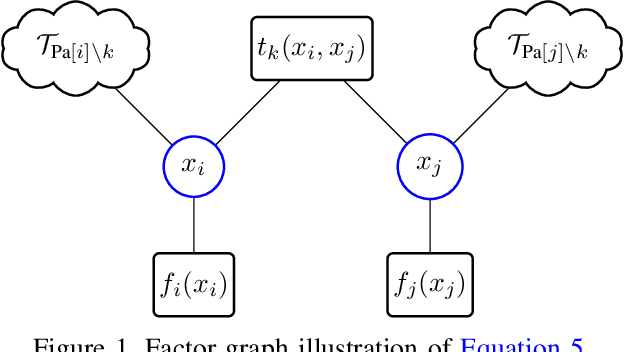
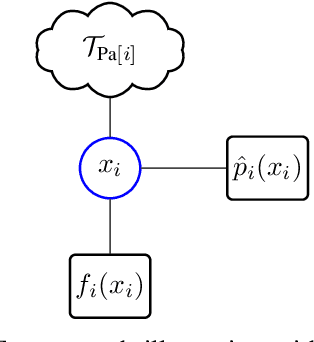
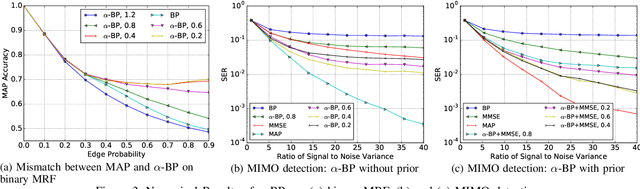
Belief propagation (BP) can do exact inference in loop-free graphs, but its performance could be poor in graphs with loops, and the understanding of its solution is limited. This work gives an interpretable belief propagation rule that is actually minimization of a localized $\alpha$-divergence. We term this algorithm as $\alpha$ belief propagation ($\alpha$-BP). The performance of $\alpha$-BP is tested in MAP (maximum a posterior) inference problems, where $\alpha$-BP can outperform (loopy) BP by a significant margin even in fully-connected graphs.