$α$ Belief Propagation for Approximate Inference

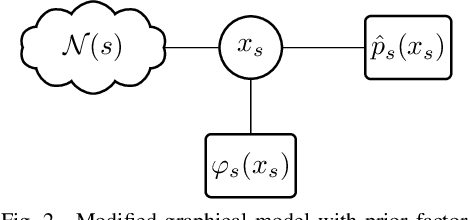
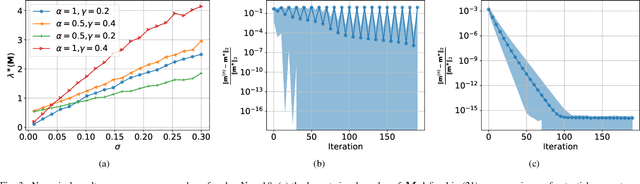
Belief propagation (BP) algorithm is a widely used message-passing method for inference in graphical models. BP on loop-free graphs converges in linear time. But for graphs with loops, BP's performance is uncertain, and the understanding of its solution is limited. To gain a better understanding of BP in general graphs, we derive an interpretable belief propagation algorithm that is motivated by minimization of a localized $\alpha$-divergence. We term this algorithm as $\alpha$ belief propagation ($\alpha$-BP). It turns out that $\alpha$-BP generalizes standard BP. In addition, this work studies the convergence properties of $\alpha$-BP. We prove and offer the convergence conditions for $\alpha$-BP. Experimental simulations on random graphs validate our theoretical results. The application of $\alpha$-BP to practical problems is also demonstrated.

Region-based Energy Neural Network for Approximate Inference

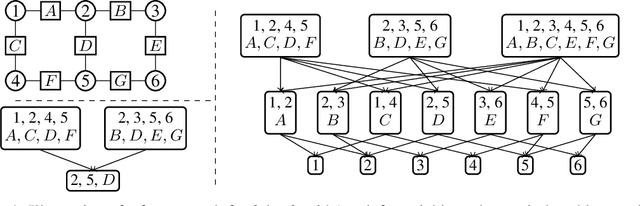
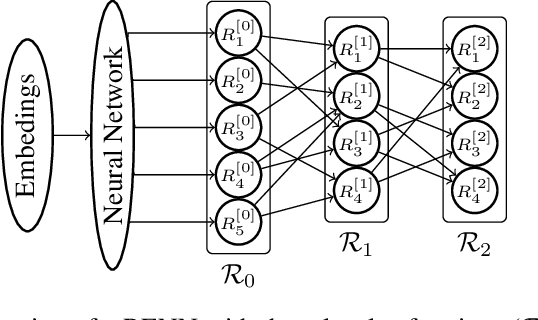
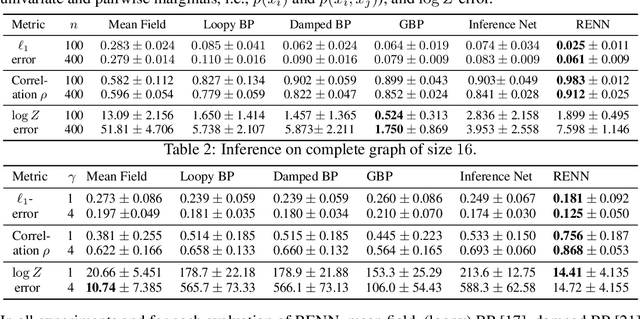
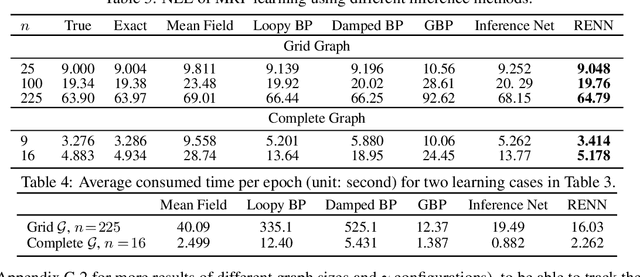
Region-based free energy was originally proposed for generalized belief propagation (GBP) to improve loopy belief propagation (loopy BP). In this paper, we propose a neural network based energy model for inference in general Markov random fields (MRFs), which directly minimizes the region-based free energy defined on region graphs. We term our model Region-based Energy Neural Network (RENN). Unlike message-passing algorithms, RENN avoids iterative message propagation and is faster. Also different from recent deep neural network based models, inference by RENN does not require sampling, and RENN works on general MRFs. RENN can also be employed for MRF learning. Our experiments on marginal distribution estimation, partition function estimation, and learning of MRFs show that RENN outperforms the mean field method, loopy BP, GBP, and the state-of-the-art neural network based model.

Powering Hidden Markov Model by Neural Network based Generative Models

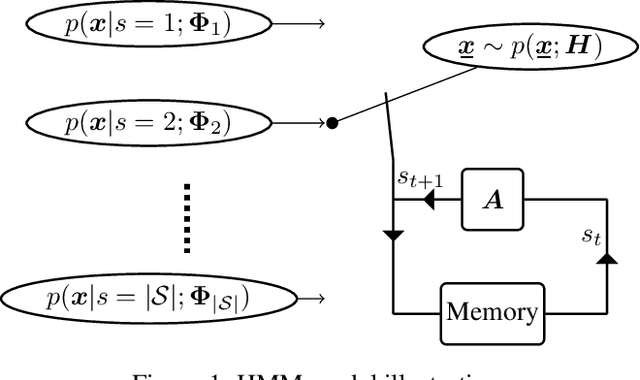
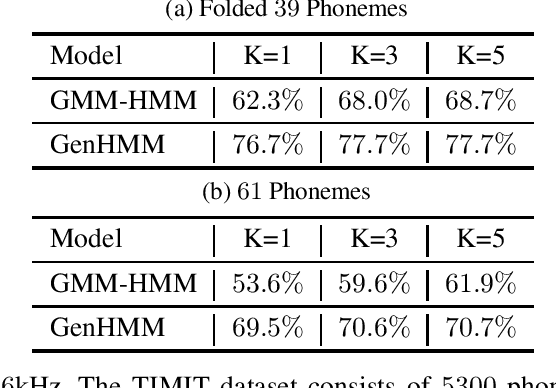
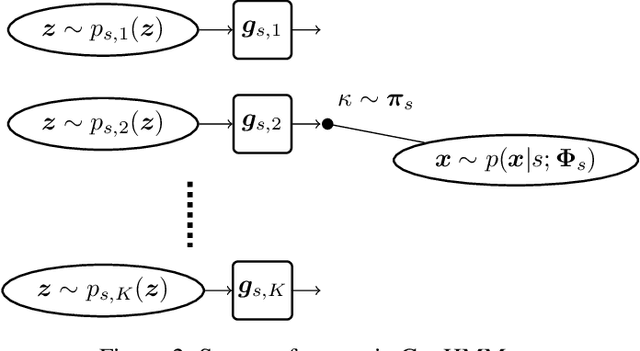
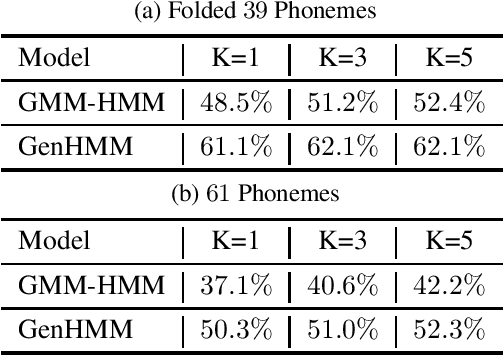
Hidden Markov model (HMM) has been successfully used for sequential data modeling problems. In this work, we propose to power the modeling capacity of HMM by bringing in neural network based generative models. The proposed model is termed as GenHMM. In the proposed GenHMM, each HMM hidden state is associated with a neural network based generative model that has tractability of exact likelihood and provides efficient likelihood computation. A generative model in GenHMM consists of mixture of generators that are realized by flow models. A learning algorithm for GenHMM is proposed in expectation-maximization framework. The convergence of the learning GenHMM is analyzed. We demonstrate the efficiency of GenHMM by classification tasks on practical sequential data.

$α$ Belief Propagation as Fully Factorized Approximation

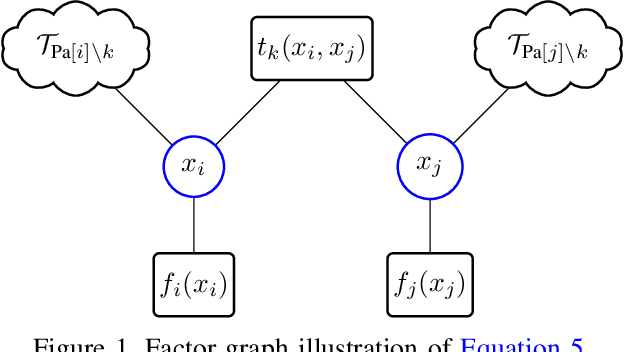
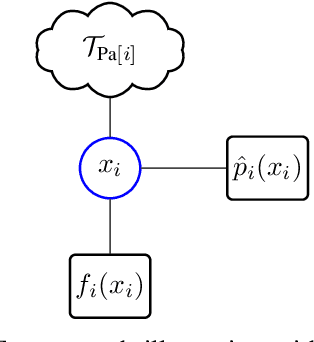
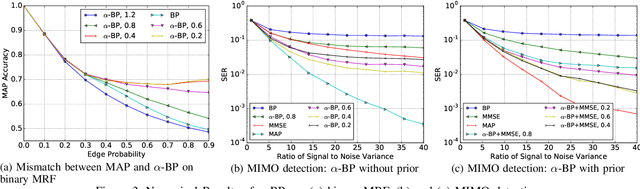
Belief propagation (BP) can do exact inference in loop-free graphs, but its performance could be poor in graphs with loops, and the understanding of its solution is limited. This work gives an interpretable belief propagation rule that is actually minimization of a localized $\alpha$-divergence. We term this algorithm as $\alpha$ belief propagation ($\alpha$-BP). The performance of $\alpha$-BP is tested in MAP (maximum a posterior) inference problems, where $\alpha$-BP can outperform (loopy) BP by a significant margin even in fully-connected graphs.

Neural Network based Explicit Mixture Models and Expectation-maximization based Learning

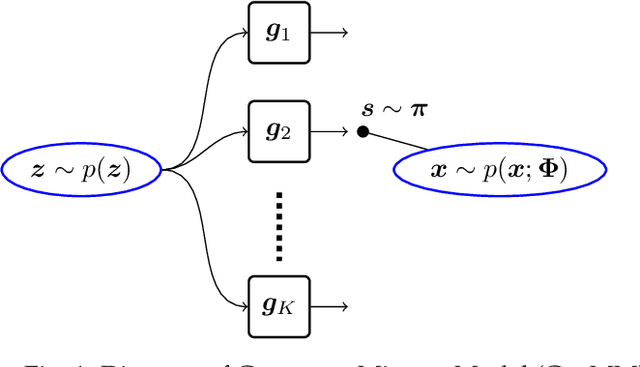
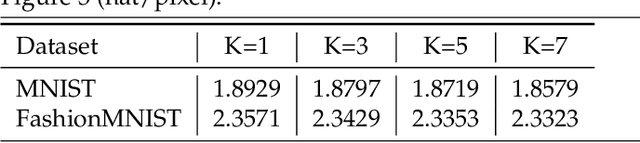
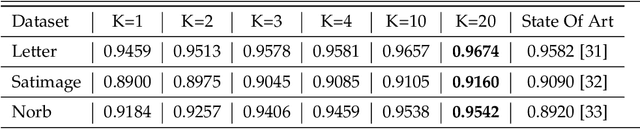
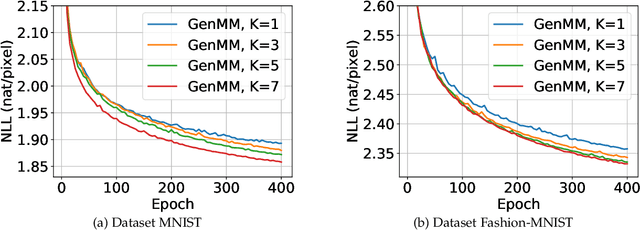
We propose two neural network based mixture models in this article. The proposed mixture models are explicit in nature. The explicit models have analytical forms with the advantages of computing likelihood and efficiency of generating samples. Computation of likelihood is an important aspect of our models. Expectation-maximization based algorithms are developed for learning parameters of the proposed models. We provide sufficient conditions to realize the expectation-maximization based learning. The main requirements are invertibility of neural networks that are used as generators and Jacobian computation of functional form of the neural networks. The requirements are practically realized using a flow-based neural network. In our first mixture model, we use multiple flow-based neural networks as generators. Naturally the model is complex. A single latent variable is used as the common input to all the neural networks. The second mixture model uses a single flow-based neural network as a generator to reduce complexity. The single generator has a latent variable input that follows a Gaussian mixture distribution. We demonstrate efficiency of proposed mixture models through extensive experiments for generating samples and maximum likelihood based classification.

Entropy-regularized Optimal Transport Generative Models

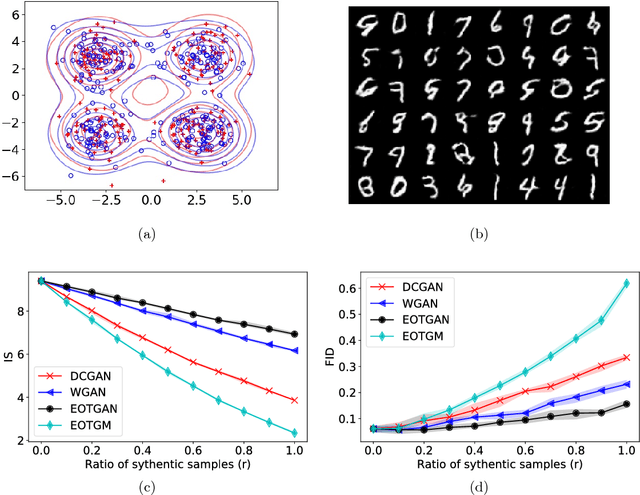
We investigate the use of entropy-regularized optimal transport (EOT) cost in developing generative models to learn implicit distributions. Two generative models are proposed. One uses EOT cost directly in an one-shot optimization problem and the other uses EOT cost iteratively in an adversarial game. The proposed generative models show improved performance over contemporary models for image generation on MNSIT.

Locally Convex Sparse Learning over Networks

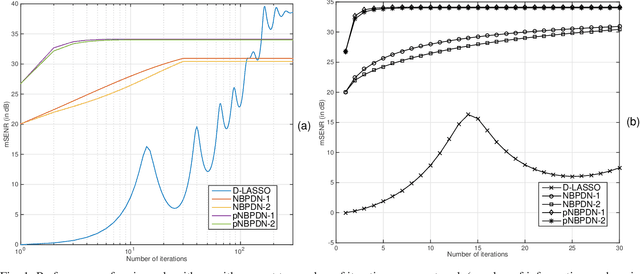
We consider a distributed learning setup where a sparse signal is estimated over a network. Our main interest is to save communication resource for information exchange over the network and reduce processing time. Each node of the network uses a convex optimization based algorithm that provides a locally optimum solution for that node. The nodes exchange their signal estimates over the network in order to refine their local estimates. At a node, the optimization algorithm is based on an $\ell_1$-norm minimization with appropriate modifications to promote sparsity as well as to include influence of estimates from neighboring nodes. Our expectation is that local estimates in each node improve fast and converge, resulting in a limited demand for communication of estimates between nodes and reducing the processing time. We provide restricted-isometry-property (RIP)-based theoretical analysis on estimation quality. In the scenario of clean observation, it is shown that the local estimates converge to the exact sparse signal under certain technical conditions. Simulation results show that the proposed algorithms show competitive performance compared to a globally optimum distributed LASSO algorithm in the sense of convergence speed and estimation error.

Estimate Exchange over Network is Good for Distributed Hard Thresholding Pursuit

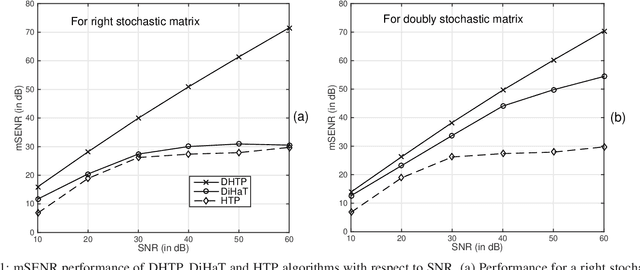
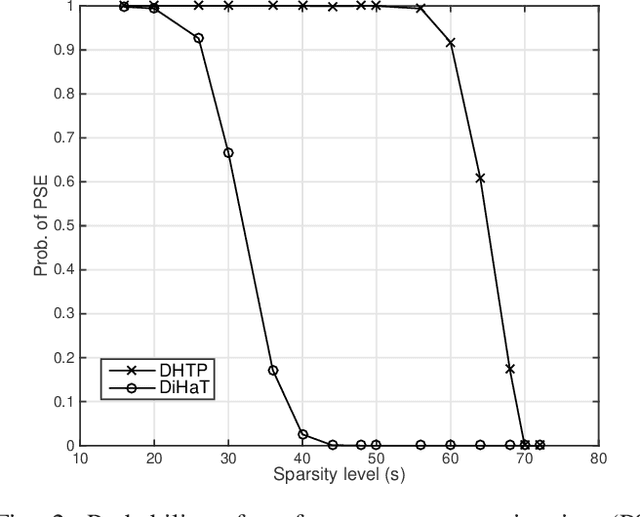
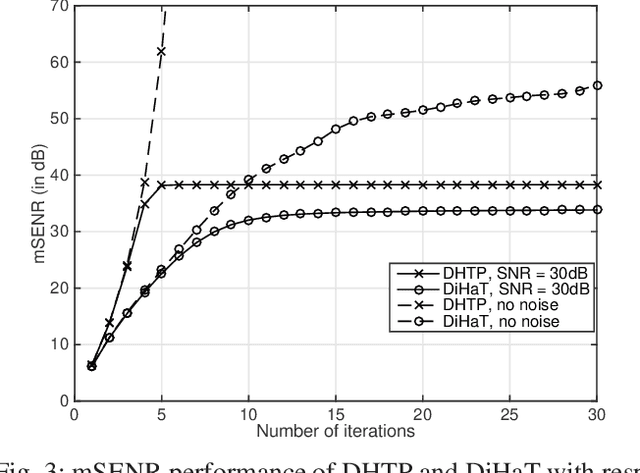
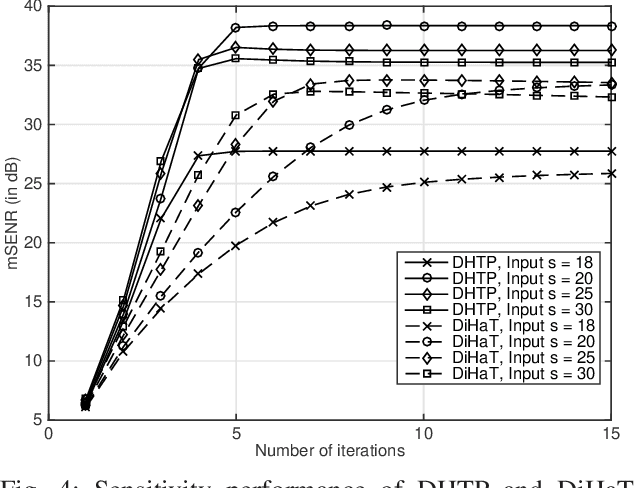
We investigate an existing distributed algorithm for learning sparse signals or data over networks. The algorithm is iterative and exchanges intermediate estimates of a sparse signal over a network. This learning strategy using exchange of intermediate estimates over the network requires a limited communication overhead for information transmission. Our objective in this article is to show that the strategy is good for learning in spite of limited communication. In pursuit of this objective, we first provide a restricted isometry property (RIP)-based theoretical analysis on convergence of the iterative algorithm. Then, using simulations, we show that the algorithm provides competitive performance in learning sparse signals vis-a-vis an existing alternate distributed algorithm. The alternate distributed algorithm exchanges more information including observations and system parameters.