A Coding-Theoretic Analysis of Hyperspherical Prototypical Learning Geometry

Hyperspherical Prototypical Learning (HPL) is a supervised approach to representation learning that designs class prototypes on the unit hypersphere. The prototypes bias the representations to class separation in a scale invariant and known geometry. Previous approaches to HPL have either of the following shortcomings: (i) they follow an unprincipled optimisation procedure; or (ii) they are theoretically sound, but are constrained to only one possible latent dimension. In this paper, we address both shortcomings. To address (i), we present a principled optimisation procedure whose solution we show is optimal. To address (ii), we construct well-separated prototypes in a wide range of dimensions using linear block codes. Additionally, we give a full characterisation of the optimal prototype placement in terms of achievable and converse bounds, showing that our proposed methods are near-optimal.

A note on generalization bounds for losses with finite moments

This paper studies the truncation method from Alquier [1] to derive high-probability PAC-Bayes bounds for unbounded losses with heavy tails. Assuming that the $p$-th moment is bounded, the resulting bounds interpolate between a slow rate $1 / \sqrt{n}$ when $p=2$, and a fast rate $1 / n$ when $p \to \infty$ and the loss is essentially bounded. Moreover, the paper derives a high-probability PAC-Bayes bound for losses with a bounded variance. This bound has an exponentially better dependence on the confidence parameter and the dependency measure than previous bounds in the literature. Finally, the paper extends all results to guarantees in expectation and single-draw PAC-Bayes. In order to so, it obtains analogues of the PAC-Bayes fast rate bound for bounded losses from [2] in these settings.

More PAC-Bayes bounds: From bounded losses, to losses with general tail behaviors, to anytime-validity

In this paper, we present new high-probability PAC-Bayes bounds for different types of losses. Firstly, for losses with a bounded range, we present a strengthened version of Catoni's bound that holds uniformly for all parameter values. This leads to new fast rate and mixed rate bounds that are interpretable and tighter than previous bounds in the literature. Secondly, for losses with more general tail behaviors, we introduce two new parameter-free bounds: a PAC-Bayes Chernoff analogue when the loss' cumulative generating function is bounded, and a bound when the loss' second moment is bounded. These two bounds are obtained using a new technique based on a discretization of the space of possible events for the "in probability" parameter optimization problem. Finally, we extend all previous results to anytime-valid bounds using a simple technique applicable to any existing bound.

Limitations of Information-Theoretic Generalization Bounds for Gradient Descent Methods in Stochastic Convex Optimization

To date, no "information-theoretic" frameworks for reasoning about generalization error have been shown to establish minimax rates for gradient descent in the setting of stochastic convex optimization. In this work, we consider the prospect of establishing such rates via several existing information-theoretic frameworks: input-output mutual information bounds, conditional mutual information bounds and variants, PAC-Bayes bounds, and recent conditional variants thereof. We prove that none of these bounds are able to establish minimax rates. We then consider a common tactic employed in studying gradient methods, whereby the final iterate is corrupted by Gaussian noise, producing a noisy "surrogate" algorithm. We prove that minimax rates cannot be established via the analysis of such surrogates. Our results suggest that new ideas are required to analyze gradient descent using information-theoretic techniques.

Tighter expected generalization error bounds via Wasserstein distance

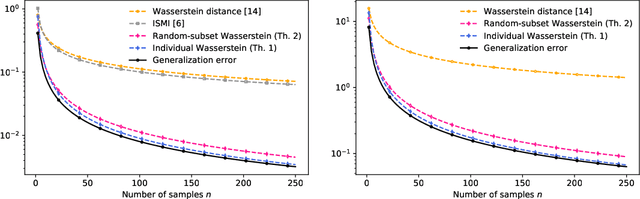
In this work, we introduce several expected generalization error bounds based on the Wasserstein distance. More precisely, we present full-dataset, single-letter, and random-subset bounds on both the standard setting and the randomized-subsample setting from Steinke and Zakynthinou [2020]. Moreover, we show that, when the loss function is bounded, these bounds recover from below (and thus are tighter than) current bounds based on the relative entropy and, for the standard setting, generate new, non-vacuous bounds also based on the relative entropy. Then, we show how similar bounds featuring the backward channel can be derived with the proposed proof techniques. Finally, we show how various new bounds based on different information measures (e.g., the lautum information or several $f$-divergences) can be derived from the presented bounds.

On Random Subset Generalization Error Bounds and the Stochastic Gradient Langevin Dynamics Algorithm

In this work, we unify several expected generalization error bounds based on random subsets using the framework developed by Hellstr\"om and Durisi [1]. First, we recover the bounds based on the individual sample mutual information from Bu et al. [2] and on a random subset of the dataset from Negrea et al. [3]. Then, we introduce their new, analogous bounds in the randomized subsample setting from Steinke and Zakynthinou [4], and we identify some limitations of the framework. Finally, we extend the bounds from Haghifam et al. [5] for Langevin dynamics to stochastic gradient Langevin dynamics and we refine them for loss functions with potentially large gradient norms.

Region-based Energy Neural Network for Approximate Inference

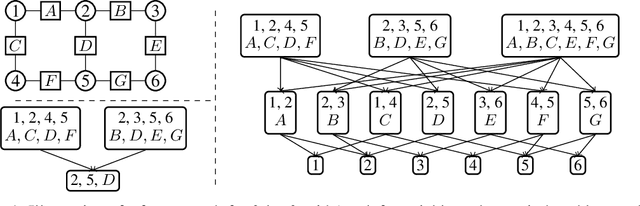
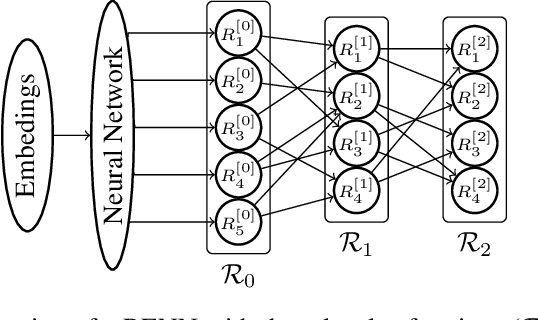
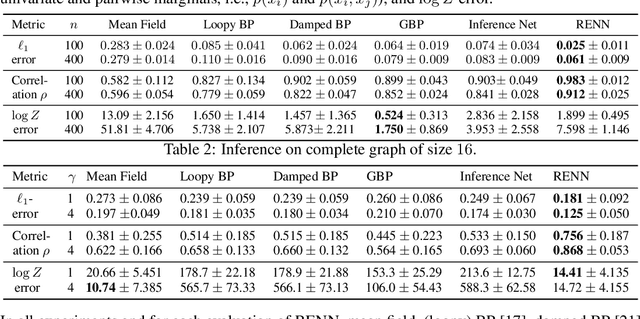
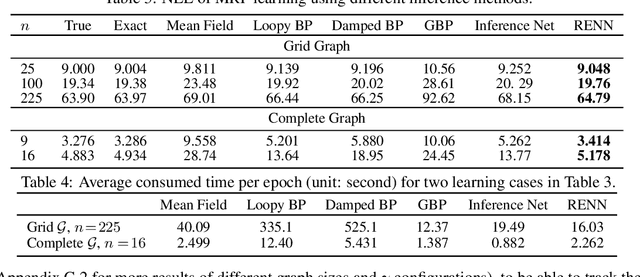
Region-based free energy was originally proposed for generalized belief propagation (GBP) to improve loopy belief propagation (loopy BP). In this paper, we propose a neural network based energy model for inference in general Markov random fields (MRFs), which directly minimizes the region-based free energy defined on region graphs. We term our model Region-based Energy Neural Network (RENN). Unlike message-passing algorithms, RENN avoids iterative message propagation and is faster. Also different from recent deep neural network based models, inference by RENN does not require sampling, and RENN works on general MRFs. RENN can also be employed for MRF learning. Our experiments on marginal distribution estimation, partition function estimation, and learning of MRFs show that RENN outperforms the mean field method, loopy BP, GBP, and the state-of-the-art neural network based model.

A Variational Approach to Privacy and Fairness

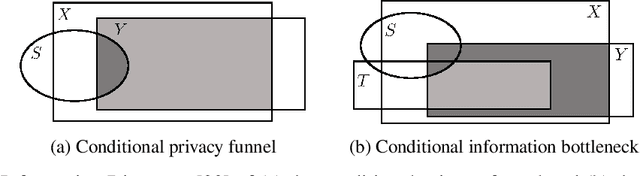
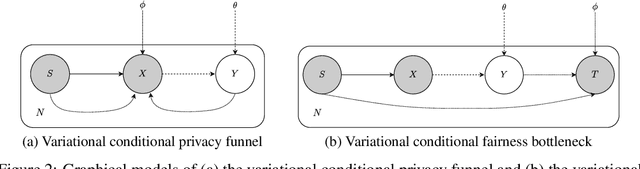
In this article, we propose a new variational approach to learn private and/or fair representations. This approach is based on the Lagrangians of a new formulation of the privacy and fairness optimization problems that we propose. In this formulation, we aim at generating representations of the data that keep a prescribed level of the relevant information that is not shared by the private or sensitive data, while minimizing the remaining information they keep. The proposed approach (i) exhibits the similarities of the privacy and fairness problems, (ii) allows us to control the trade-off between utility and privacy or fairness through the Lagrange multiplier parameter, and (iii) can be comfortably incorporated to common representation learning algorithms such as the VAE, the $\beta$-VAE, the VIB, or the nonlinear IB.

The Convex Information Bottleneck Lagrangian

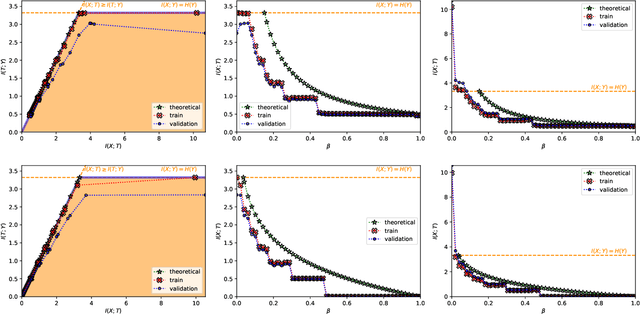
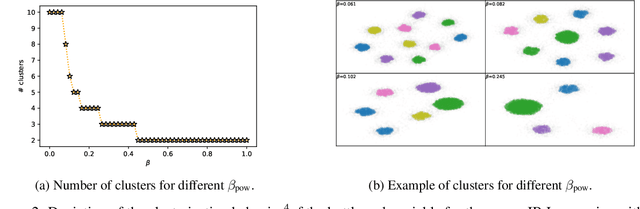
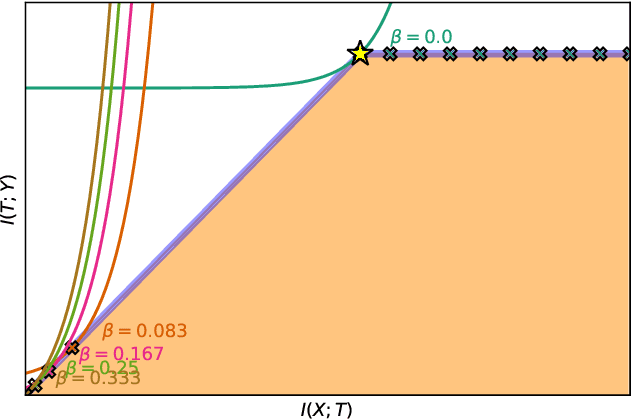
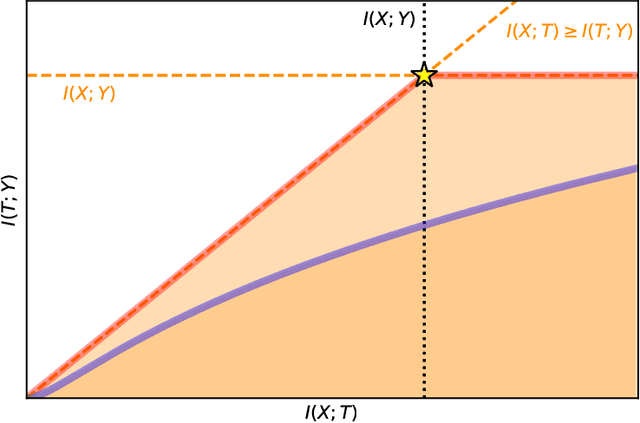
The information bottleneck (IB) problem tackles the issue of obtaining relevant compressed representations $T$ of some random variable $X$ for the task of predicting $Y$. It is defined as a constrained optimization problem which maximizes the information the representation has about the task, $I(T;Y)$, while ensuring that a certain level of compression $r$ is achieved (i.e., $ I(X;T) \leq r$). For practical reasons, the problem is usually solved by maximizing the IB Lagrangian (i.e., $\mathcal{L}_{\text{IB}}(T;\beta) = I(T;Y) - \beta I(X;T)$) for many values of $\beta \in [0,1]$. Then, the curve of maximal $I(T;Y)$ for a given $I(X;T)$ is drawn and a representation with the desired predictability and compression is selected. It is known when $Y$ is a deterministic function of $X$, the IB curve cannot be explored and another Lagrangian has been proposed to tackle this problem: the squared IB Lagrangian: $\mathcal{L}_{\text{sq-IB}}(T;\beta_{\text{sq}})=I(T;Y)-\beta_{\text{sq}}I(X;T)^2$. In this paper, we (i) present a general family of Lagrangians which allow for the exploration of the IB curve in all scenarios; (ii) provide the exact one-to-one mapping between the Lagrange multiplier and the desired compression rate $r$ for known IB curve shapes; and (iii) show we can approximately obtain a specific compression level with the convex IB Lagrangian for both known and unknown IB curve shapes. This eliminates the burden of solving the optimization problem for many values of the Lagrange multiplier. That is, we prove that we can solve the original constrained problem with a single optimization.