Tighter expected generalization error bounds via Wasserstein distance
Paper and Code
Jan 22, 2021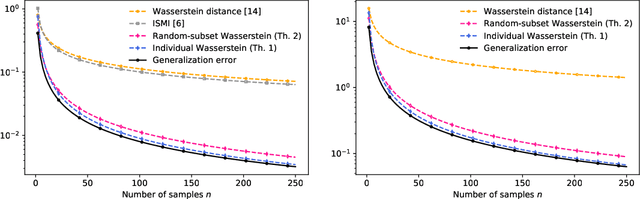
In this work, we introduce several expected generalization error bounds based on the Wasserstein distance. More precisely, we present full-dataset, single-letter, and random-subset bounds on both the standard setting and the randomized-subsample setting from Steinke and Zakynthinou [2020]. Moreover, we show that, when the loss function is bounded, these bounds recover from below (and thus are tighter than) current bounds based on the relative entropy and, for the standard setting, generate new, non-vacuous bounds also based on the relative entropy. Then, we show how similar bounds featuring the backward channel can be derived with the proposed proof techniques. Finally, we show how various new bounds based on different information measures (e.g., the lautum information or several $f$-divergences) can be derived from the presented bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge