The Convex Information Bottleneck Lagrangian
Paper and Code
Jan 10, 2020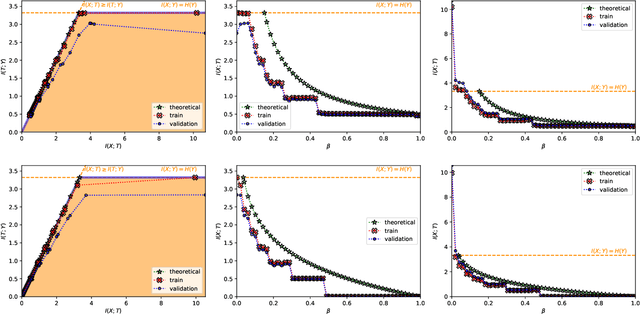
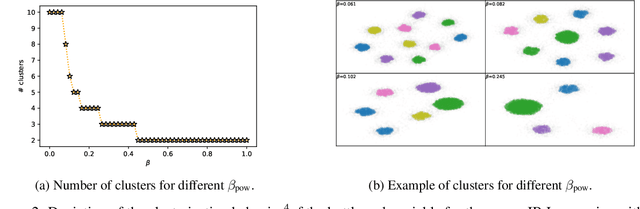
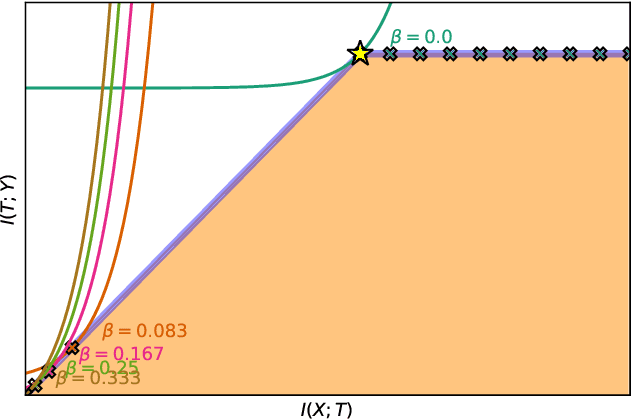
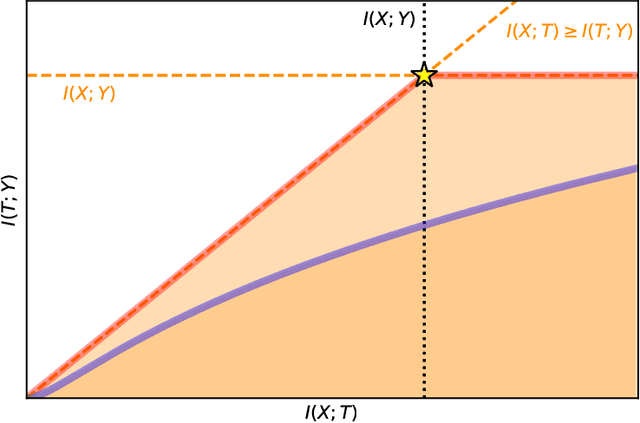
The information bottleneck (IB) problem tackles the issue of obtaining relevant compressed representations $T$ of some random variable $X$ for the task of predicting $Y$. It is defined as a constrained optimization problem which maximizes the information the representation has about the task, $I(T;Y)$, while ensuring that a certain level of compression $r$ is achieved (i.e., $ I(X;T) \leq r$). For practical reasons, the problem is usually solved by maximizing the IB Lagrangian (i.e., $\mathcal{L}_{\text{IB}}(T;\beta) = I(T;Y) - \beta I(X;T)$) for many values of $\beta \in [0,1]$. Then, the curve of maximal $I(T;Y)$ for a given $I(X;T)$ is drawn and a representation with the desired predictability and compression is selected. It is known when $Y$ is a deterministic function of $X$, the IB curve cannot be explored and another Lagrangian has been proposed to tackle this problem: the squared IB Lagrangian: $\mathcal{L}_{\text{sq-IB}}(T;\beta_{\text{sq}})=I(T;Y)-\beta_{\text{sq}}I(X;T)^2$. In this paper, we (i) present a general family of Lagrangians which allow for the exploration of the IB curve in all scenarios; (ii) provide the exact one-to-one mapping between the Lagrange multiplier and the desired compression rate $r$ for known IB curve shapes; and (iii) show we can approximately obtain a specific compression level with the convex IB Lagrangian for both known and unknown IB curve shapes. This eliminates the burden of solving the optimization problem for many values of the Lagrange multiplier. That is, we prove that we can solve the original constrained problem with a single optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge