A Variational Approach to Privacy and Fairness
Paper and Code
Jun 11, 2020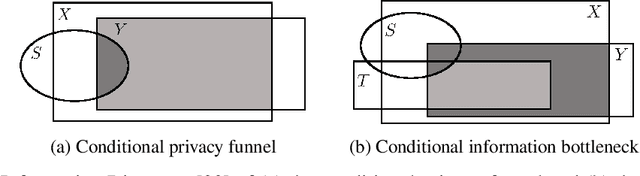
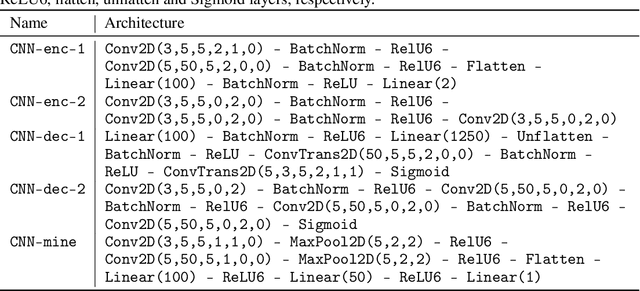
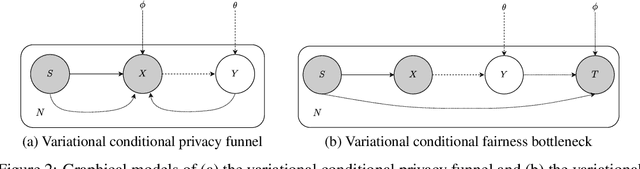
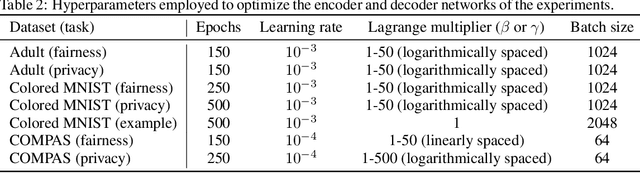
In this article, we propose a new variational approach to learn private and/or fair representations. This approach is based on the Lagrangians of a new formulation of the privacy and fairness optimization problems that we propose. In this formulation, we aim at generating representations of the data that keep a prescribed level of the relevant information that is not shared by the private or sensitive data, while minimizing the remaining information they keep. The proposed approach (i) exhibits the similarities of the privacy and fairness problems, (ii) allows us to control the trade-off between utility and privacy or fairness through the Lagrange multiplier parameter, and (iii) can be comfortably incorporated to common representation learning algorithms such as the VAE, the $\beta$-VAE, the VIB, or the nonlinear IB.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge