$α$ Belief Propagation for Approximate Inference

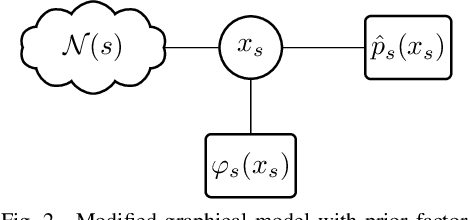
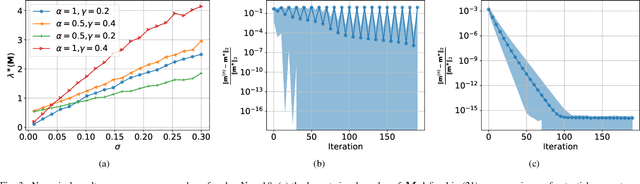
Belief propagation (BP) algorithm is a widely used message-passing method for inference in graphical models. BP on loop-free graphs converges in linear time. But for graphs with loops, BP's performance is uncertain, and the understanding of its solution is limited. To gain a better understanding of BP in general graphs, we derive an interpretable belief propagation algorithm that is motivated by minimization of a localized $\alpha$-divergence. We term this algorithm as $\alpha$ belief propagation ($\alpha$-BP). It turns out that $\alpha$-BP generalizes standard BP. In addition, this work studies the convergence properties of $\alpha$-BP. We prove and offer the convergence conditions for $\alpha$-BP. Experimental simulations on random graphs validate our theoretical results. The application of $\alpha$-BP to practical problems is also demonstrated.

Neural Network based Explicit Mixture Models and Expectation-maximization based Learning

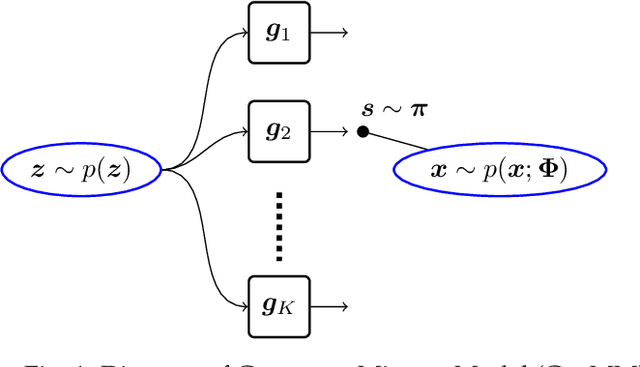
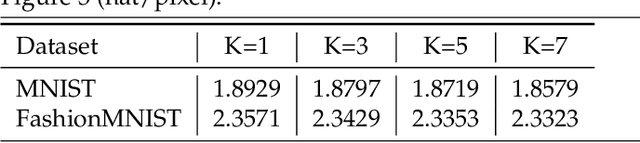
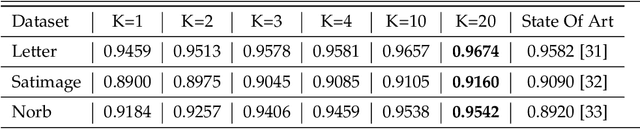
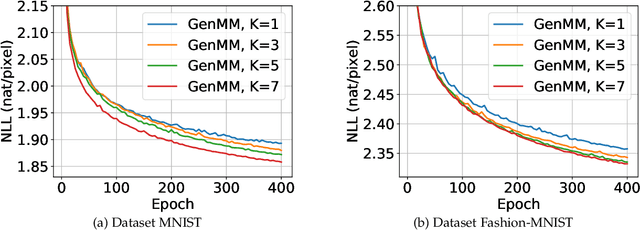
We propose two neural network based mixture models in this article. The proposed mixture models are explicit in nature. The explicit models have analytical forms with the advantages of computing likelihood and efficiency of generating samples. Computation of likelihood is an important aspect of our models. Expectation-maximization based algorithms are developed for learning parameters of the proposed models. We provide sufficient conditions to realize the expectation-maximization based learning. The main requirements are invertibility of neural networks that are used as generators and Jacobian computation of functional form of the neural networks. The requirements are practically realized using a flow-based neural network. In our first mixture model, we use multiple flow-based neural networks as generators. Naturally the model is complex. A single latent variable is used as the common input to all the neural networks. The second mixture model uses a single flow-based neural network as a generator to reduce complexity. The single generator has a latent variable input that follows a Gaussian mixture distribution. We demonstrate efficiency of proposed mixture models through extensive experiments for generating samples and maximum likelihood based classification.

Entropy-regularized Optimal Transport Generative Models

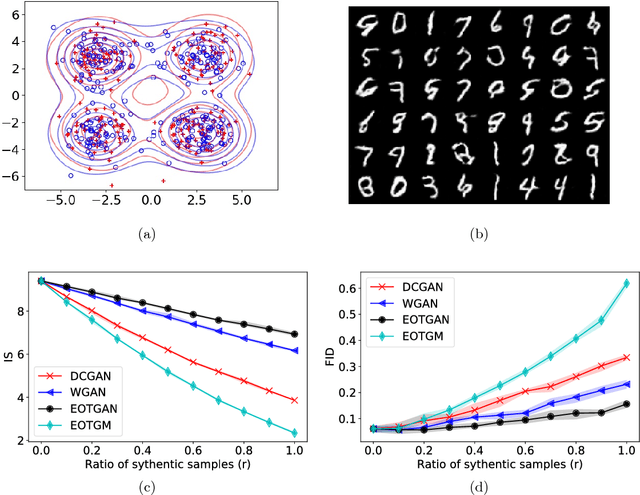
We investigate the use of entropy-regularized optimal transport (EOT) cost in developing generative models to learn implicit distributions. Two generative models are proposed. One uses EOT cost directly in an one-shot optimization problem and the other uses EOT cost iteratively in an adversarial game. The proposed generative models show improved performance over contemporary models for image generation on MNSIT.