Zuxing Li
$α$ Belief Propagation for Approximate Inference
Jun 27, 2020
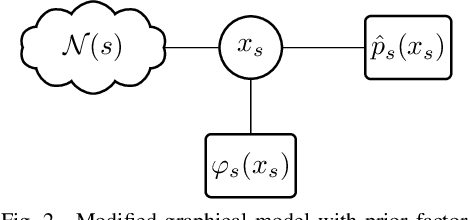
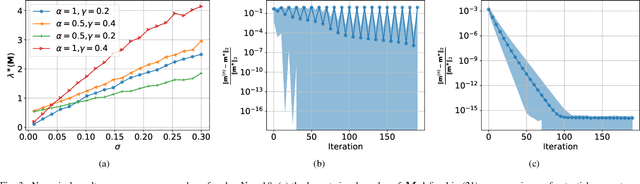

Abstract:Belief propagation (BP) algorithm is a widely used message-passing method for inference in graphical models. BP on loop-free graphs converges in linear time. But for graphs with loops, BP's performance is uncertain, and the understanding of its solution is limited. To gain a better understanding of BP in general graphs, we derive an interpretable belief propagation algorithm that is motivated by minimization of a localized $\alpha$-divergence. We term this algorithm as $\alpha$ belief propagation ($\alpha$-BP). It turns out that $\alpha$-BP generalizes standard BP. In addition, this work studies the convergence properties of $\alpha$-BP. We prove and offer the convergence conditions for $\alpha$-BP. Experimental simulations on random graphs validate our theoretical results. The application of $\alpha$-BP to practical problems is also demonstrated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge