Skeletonization of neuronal processes using Discrete Morse techniques from computational topology

To understand biological intelligence we need to map neuronal networks in vertebrate brains. Mapping mesoscale neural circuitry is done using injections of tracers that label groups of neurons whose axons project to different brain regions. Since many neurons are labeled, it is difficult to follow individual axons. Previous approaches have instead quantified the regional projections using the total label intensity within a region. However, such a quantification is not biologically meaningful. We propose a new approach better connected to the underlying neurons by skeletonizing labeled axon fragments and then estimating a volumetric length density. Our approach uses a combination of deep nets and the Discrete Morse (DM) technique from computational topology. This technique takes into account nonlocal connectivity information and therefore provides noise-robustness. We demonstrate the utility and scalability of the approach on whole-brain tracer injected data. We also define and illustrate an information theoretic measure that quantifies the additional information obtained, compared to the skeletonized tracer injection fragments, when individual axon morphologies are available. Our approach is the first application of the DM technique to computational neuroanatomy. It can help bridge between single-axon skeletons and tracer injections, two important data types in mapping neural networks in vertebrates.

Detection and skeletonization of single neurons and tracer injections using topological methods

Neuroscientific data analysis has traditionally relied on linear algebra and stochastic process theory. However, the tree-like shapes of neurons cannot be described easily as points in a vector space (the subtraction of two neuronal shapes is not a meaningful operation), and methods from computational topology are better suited to their analysis. Here we introduce methods from Discrete Morse (DM) Theory to extract the tree-skeletons of individual neurons from volumetric brain image data, and to summarize collections of neurons labelled by tracer injections. Since individual neurons are topologically trees, it is sensible to summarize the collection of neurons using a consensus tree-shape that provides a richer information summary than the traditional regional 'connectivity matrix' approach. The conceptually elegant DM approach lacks hand-tuned parameters and captures global properties of the data as opposed to previous approaches which are inherently local. For individual skeletonization of sparsely labelled neurons we obtain substantial performance gains over state-of-the-art non-topological methods (over 10% improvements in precision and faster proofreading). The consensus-tree summary of tracer injections incorporates the regional connectivity matrix information, but in addition captures the collective collateral branching patterns of the set of neurons connected to the injection site, and provides a bridge between single-neuron morphology and tracer-injection data.

SSFN: Self Size-estimating Feed-forward Network and Low Complexity Design

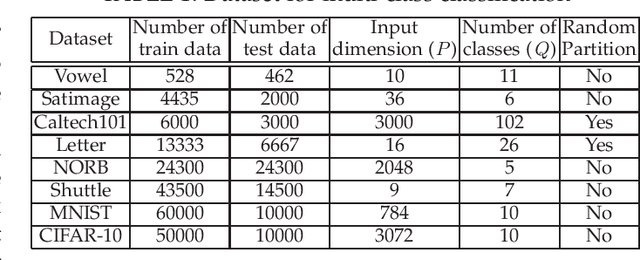
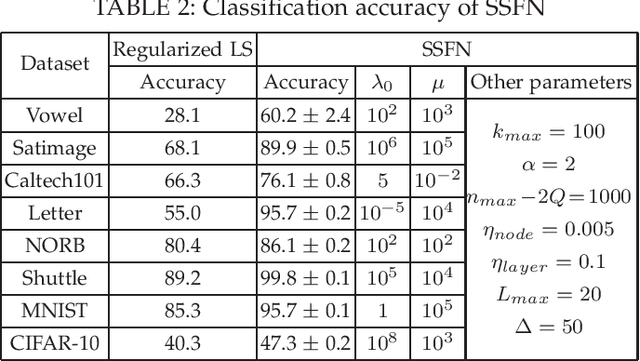
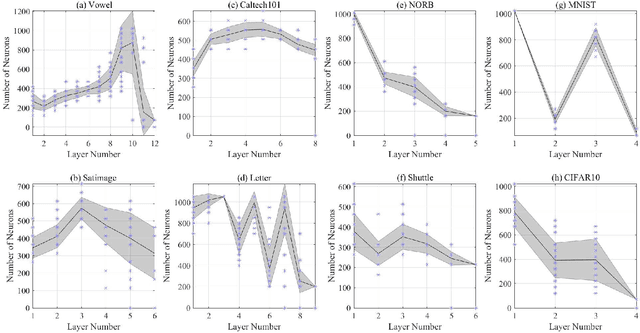
We design a self size-estimating feed-forward network (SSFN) using a joint optimization approach for estimation of number of layers, number of nodes and learning of weight matrices at a low computational complexity. In the proposed approach, SSFN grows from a small-size network to a large-size network. The increase in size from small-size to large-size guarantees a monotonically decreasing cost with addition of nodes and layers. The optimization approach uses a sequence of layer-wise target-seeking non-convex optimization problems. Using `lossless flow property' of some activation functions, such as rectified linear unit (ReLU), we analytically find regularization parameters in the layer-wise non-convex optimization problems. Closed-form analytic expressions of regularization parameters allow to avoid tedious cross-validations. The layer-wise non-convex optimization problems are further relaxed to convex optimization problems for ease of implementation and analytical tractability. The convex relaxation helps to design a low-complexity algorithm for construction of the SSFN. We experiment with eight popular benchmark datasets for sound and image classification tasks. Using extensive experiments we show that the SSFN can self-estimate its size using the low-complexity algorithm. The size of SSFN varies significantly across the eight datasets.

Locally Convex Sparse Learning over Networks

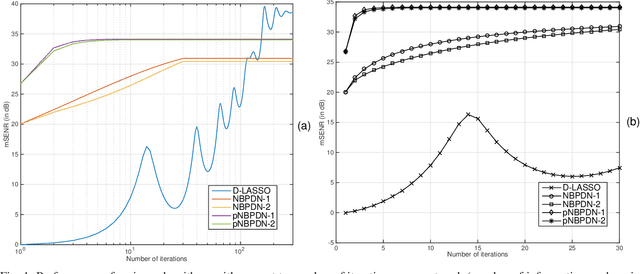
We consider a distributed learning setup where a sparse signal is estimated over a network. Our main interest is to save communication resource for information exchange over the network and reduce processing time. Each node of the network uses a convex optimization based algorithm that provides a locally optimum solution for that node. The nodes exchange their signal estimates over the network in order to refine their local estimates. At a node, the optimization algorithm is based on an $\ell_1$-norm minimization with appropriate modifications to promote sparsity as well as to include influence of estimates from neighboring nodes. Our expectation is that local estimates in each node improve fast and converge, resulting in a limited demand for communication of estimates between nodes and reducing the processing time. We provide restricted-isometry-property (RIP)-based theoretical analysis on estimation quality. In the scenario of clean observation, it is shown that the local estimates converge to the exact sparse signal under certain technical conditions. Simulation results show that the proposed algorithms show competitive performance compared to a globally optimum distributed LASSO algorithm in the sense of convergence speed and estimation error.

Progressive Learning for Systematic Design of Large Neural Networks

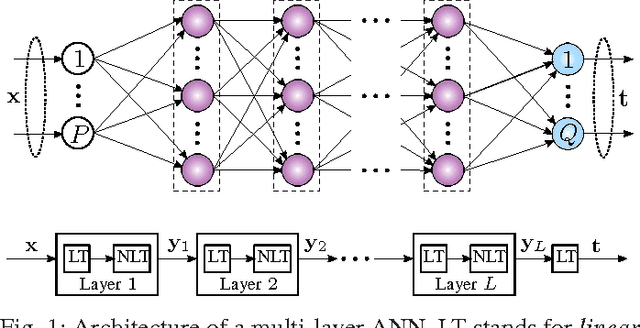
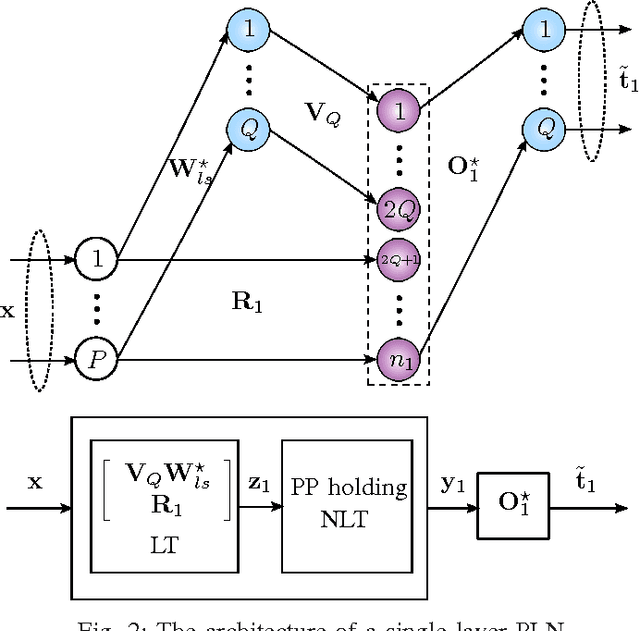
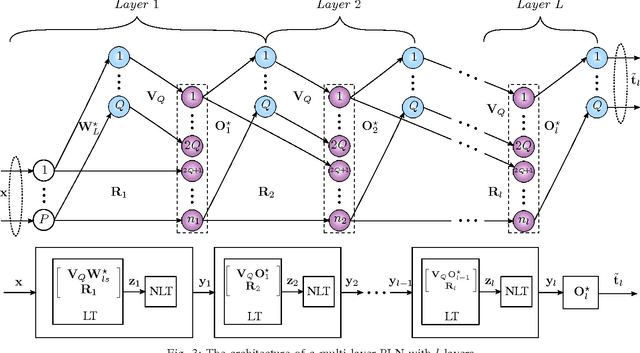
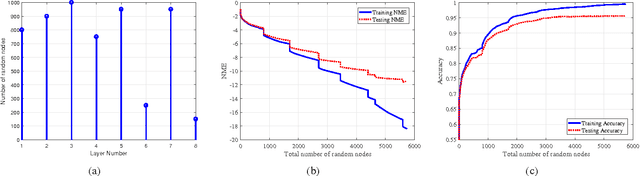
We develop an algorithm for systematic design of a large artificial neural network using a progression property. We find that some non-linear functions, such as the rectifier linear unit and its derivatives, hold the property. The systematic design addresses the choice of network size and regularization of parameters. The number of nodes and layers in network increases in progression with the objective of consistently reducing an appropriate cost. Each layer is optimized at a time, where appropriate parameters are learned using convex optimization. Regularization parameters for convex optimization do not need a significant manual effort for tuning. We also use random instances for some weight matrices, and that helps to reduce the number of parameters we learn. The developed network is expected to show good generalization power due to appropriate regularization and use of random weights in the layers. This expectation is verified by extensive experiments for classification and regression problems, using standard databases.

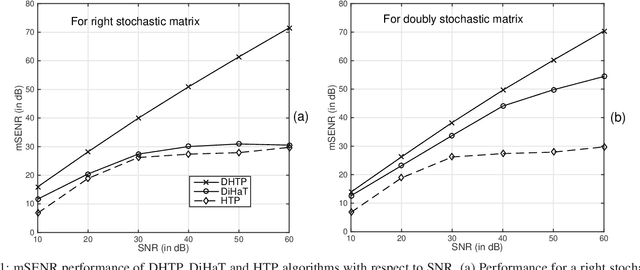
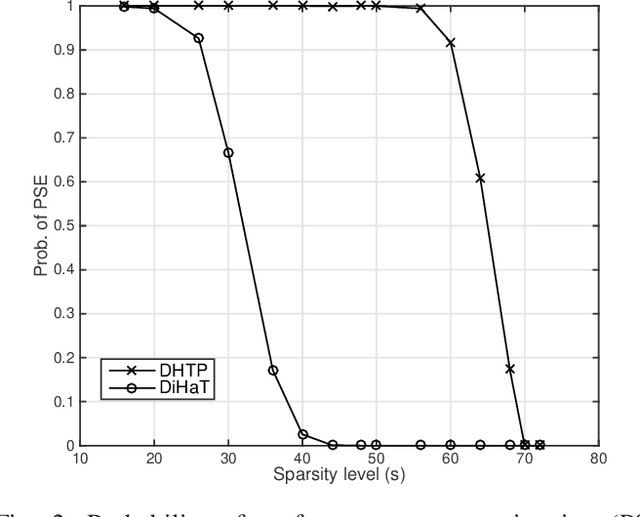
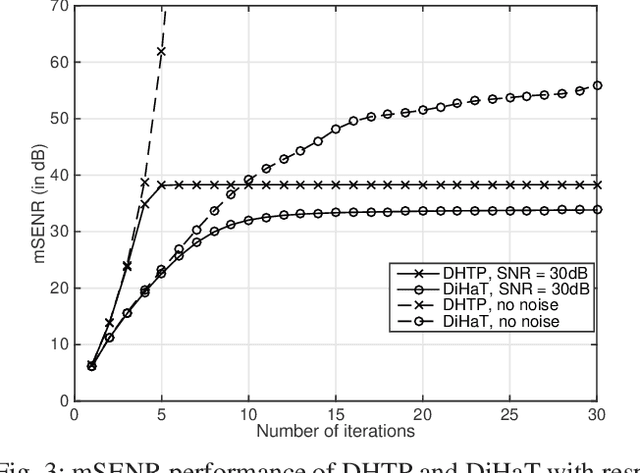
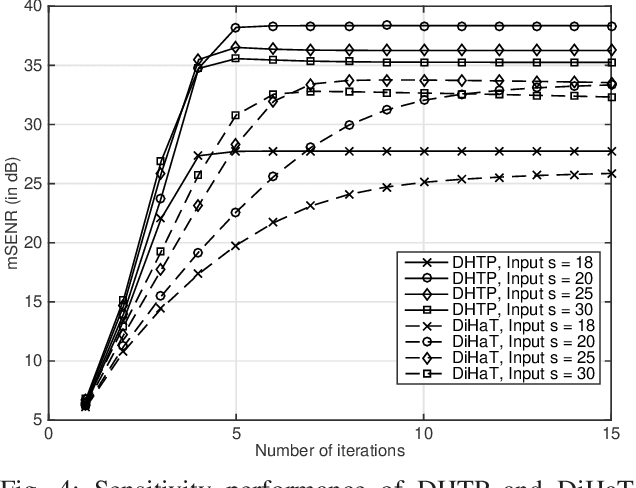
Estimate Exchange over Network is Good for Distributed Hard Thresholding Pursuit

We investigate an existing distributed algorithm for learning sparse signals or data over networks. The algorithm is iterative and exchanges intermediate estimates of a sparse signal over a network. This learning strategy using exchange of intermediate estimates over the network requires a limited communication overhead for information transmission. Our objective in this article is to show that the strategy is good for learning in spite of limited communication. In pursuit of this objective, we first provide a restricted isometry property (RIP)-based theoretical analysis on convergence of the iterative algorithm. Then, using simulations, we show that the algorithm provides competitive performance in learning sparse signals vis-a-vis an existing alternate distributed algorithm. The alternate distributed algorithm exchanges more information including observations and system parameters.