Neural Greedy Pursuit for Feature Selection

We propose a greedy algorithm to select $N$ important features among $P$ input features for a non-linear prediction problem. The features are selected one by one sequentially, in an iterative loss minimization procedure. We use neural networks as predictors in the algorithm to compute the loss and hence, we refer to our method as neural greedy pursuit (NGP). NGP is efficient in selecting $N$ features when $N \ll P$, and it provides a notion of feature importance in a descending order following the sequential selection procedure. We experimentally show that NGP provides better performance than several feature selection methods such as DeepLIFT and Drop-one-out loss. In addition, we experimentally show a phase transition behavior in which perfect selection of all $N$ features without false positives is possible when the training data size exceeds a threshold.

Use of Deterministic Transforms to Design Weight Matrices of a Neural Network

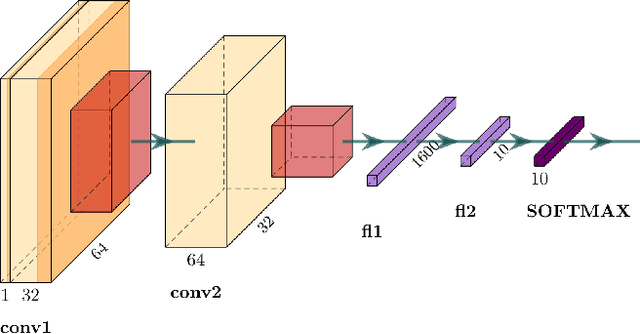
Self size-estimating feedforward network (SSFN) is a feedforward multilayer network. For the existing SSFN, a part of each weight matrix is trained using a layer-wise convex optimization approach (a supervised training), while the other part is chosen as a random matrix instance (an unsupervised training). In this article, the use of deterministic transforms instead of random matrix instances for the SSFN weight matrices is explored. The use of deterministic transforms provides a reduction in computational complexity. The use of several deterministic transforms is investigated, such as discrete cosine transform, Hadamard transform, Hartley transform, and wavelet transforms. The choice of a deterministic transform among a set of transforms is made in an unsupervised manner. To this end, two methods based on features' statistical parameters are developed. The proposed methods help to design a neural net where deterministic transforms can vary across its layers' weight matrices. The effectiveness of the proposed approach vis-a-vis the SSFN is illustrated for object classification tasks using several benchmark datasets.

Statistical model-based evaluation of neural networks

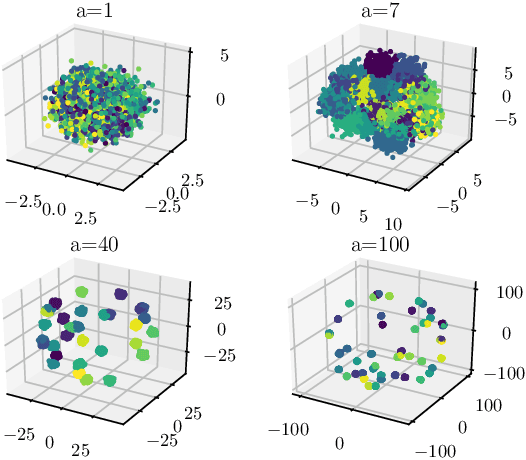
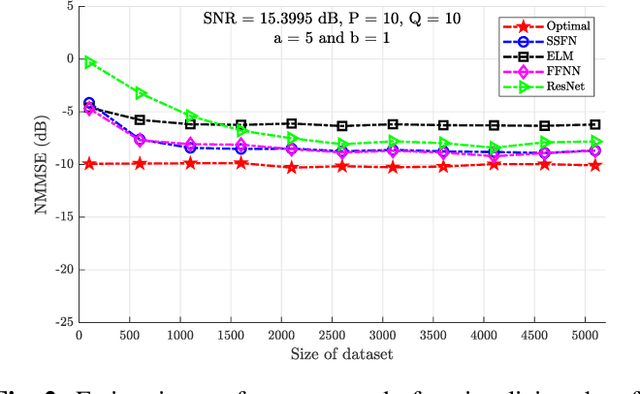
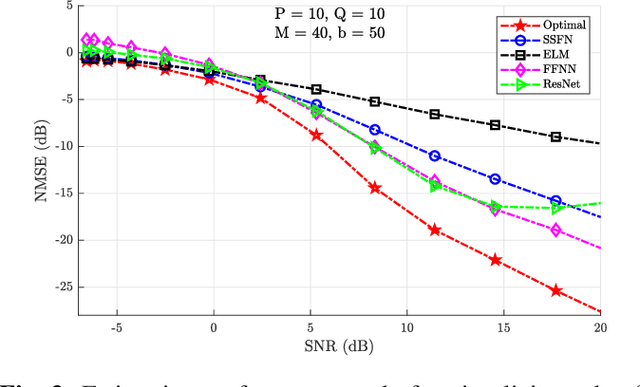
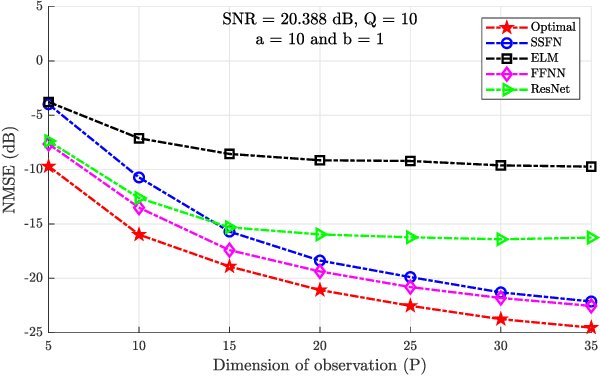
Using a statistical model-based data generation, we develop an experimental setup for the evaluation of neural networks (NNs). The setup helps to benchmark a set of NNs vis-a-vis minimum-mean-square-error (MMSE) performance bounds. This allows us to test the effects of training data size, data dimension, data geometry, noise, and mismatch between training and testing conditions. In the proposed setup, we use a Gaussian mixture distribution to generate data for training and testing a set of competing NNs. Our experiments show the importance of understanding the type and statistical conditions of data for appropriate application and design of NNs

A ReLU Dense Layer to Improve the Performance of Neural Networks

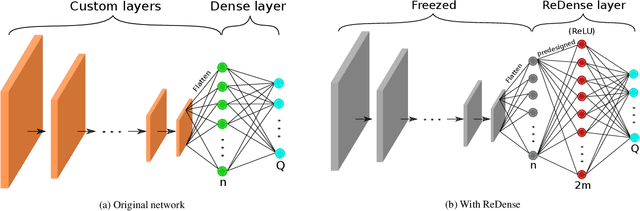
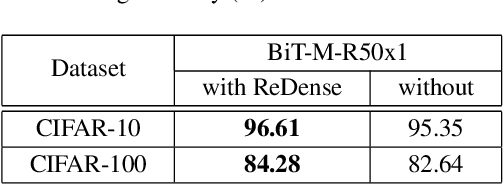
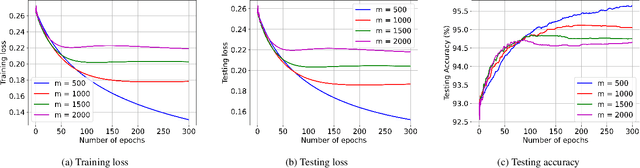
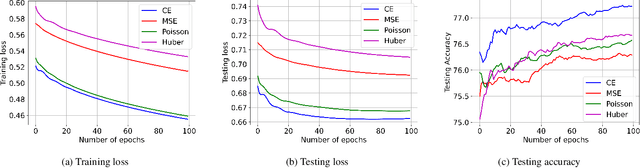
We propose ReDense as a simple and low complexity way to improve the performance of trained neural networks. We use a combination of random weights and rectified linear unit (ReLU) activation function to add a ReLU dense (ReDense) layer to the trained neural network such that it can achieve a lower training loss. The lossless flow property (LFP) of ReLU is the key to achieve the lower training loss while keeping the generalization error small. ReDense does not suffer from vanishing gradient problem in the training due to having a shallow structure. We experimentally show that ReDense can improve the training and testing performance of various neural network architectures with different optimization loss and activation functions. Finally, we test ReDense on some of the state-of-the-art architectures and show the performance improvement on benchmark datasets.

A Low Complexity Decentralized Neural Net with Centralized Equivalence using Layer-wise Learning

We design a low complexity decentralized learning algorithm to train a recently proposed large neural network in distributed processing nodes (workers). We assume the communication network between the workers is synchronized and can be modeled as a doubly-stochastic mixing matrix without having any master node. In our setup, the training data is distributed among the workers but is not shared in the training process due to privacy and security concerns. Using alternating-direction-method-of-multipliers (ADMM) along with a layerwise convex optimization approach, we propose a decentralized learning algorithm which enjoys low computational complexity and communication cost among the workers. We show that it is possible to achieve equivalent learning performance as if the data is available in a single place. Finally, we experimentally illustrate the time complexity and convergence behavior of the algorithm.

Predictive Analysis of COVID-19 Time-series Data from Johns Hopkins University

We provide a predictive analysis of the spread of COVID-19, also known as SARS-CoV-2, using the dataset made publicly available online by the Johns Hopkins University. Our main objective is to provide predictions of the number of infected people for different countries in the next 14 days. The predictive analysis is done using time-series data transformed on a logarithmic scale. We use two well-known methods for prediction: polynomial regression and neural network. As the number of training data for each country is limited, we use a single-layer neural network called the extreme learning machine (ELM) to avoid over-fitting. Due to the non-stationary nature of the time-series, a sliding window approach is used to provide a more accurate prediction.

Asynchronous Decentralized Learning of a Neural Network

In this work, we exploit an asynchronous computing framework namely ARock to learn a deep neural network called self-size estimating feedforward neural network (SSFN) in a decentralized scenario. Using this algorithm namely asynchronous decentralized SSFN (dSSFN), we provide the centralized equivalent solution under certain technical assumptions. Asynchronous dSSFN relaxes the communication bottleneck by allowing one node activation and one side communication, which reduces the communication overhead significantly, consequently increasing the learning speed. We compare asynchronous dSSFN with traditional synchronous dSSFN in the experimental results, which shows the competitive performance of asynchronous dSSFN, especially when the communication network is sparse.

High-dimensional Neural Feature using Rectified Linear Unit and Random Matrix Instance

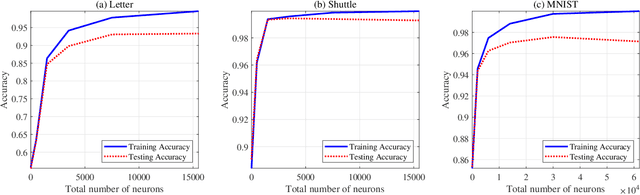
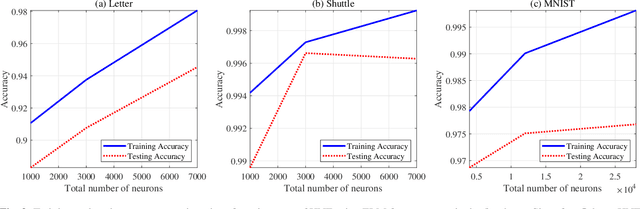
We design a ReLU-based multilayer neural network to generate a rich high-dimensional feature vector. The feature guarantees a monotonically decreasing training cost as the number of layers increases. We design the weight matrix in each layer to extend the feature vectors to a higher dimensional space while providing a richer representation in the sense of training cost. Linear projection to the target in the higher dimensional space leads to a lower training cost if a convex cost is minimized. An $\ell_2$-norm convex constraint is used in the minimization to improve the generalization error and avoid overfitting. The regularization hyperparameters of the network are derived analytically to guarantee a monotonic decrement of the training cost and therefore, it eliminates the need for cross-validation to find the regularization hyperparameter in each layer.

SSFN: Self Size-estimating Feed-forward Network and Low Complexity Design

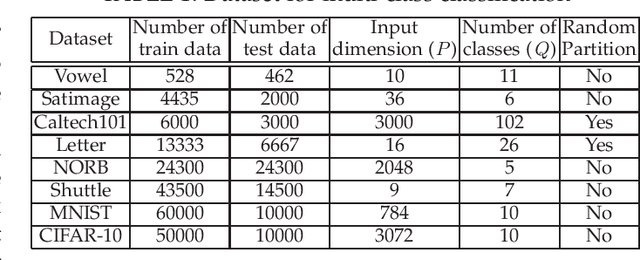
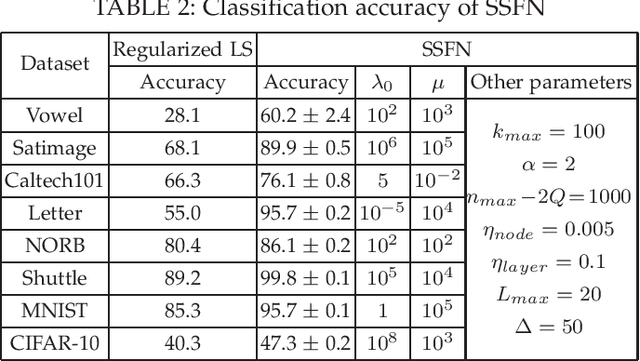
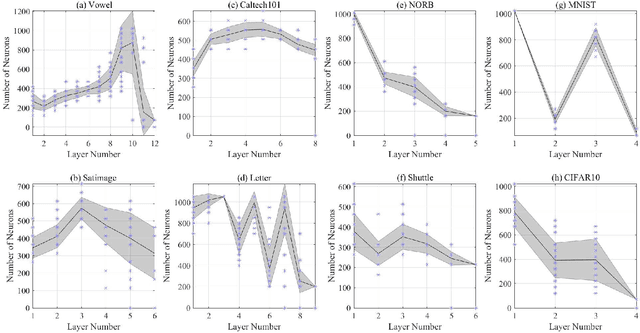
We design a self size-estimating feed-forward network (SSFN) using a joint optimization approach for estimation of number of layers, number of nodes and learning of weight matrices at a low computational complexity. In the proposed approach, SSFN grows from a small-size network to a large-size network. The increase in size from small-size to large-size guarantees a monotonically decreasing cost with addition of nodes and layers. The optimization approach uses a sequence of layer-wise target-seeking non-convex optimization problems. Using `lossless flow property' of some activation functions, such as rectified linear unit (ReLU), we analytically find regularization parameters in the layer-wise non-convex optimization problems. Closed-form analytic expressions of regularization parameters allow to avoid tedious cross-validations. The layer-wise non-convex optimization problems are further relaxed to convex optimization problems for ease of implementation and analytical tractability. The convex relaxation helps to design a low-complexity algorithm for construction of the SSFN. We experiment with eight popular benchmark datasets for sound and image classification tasks. Using extensive experiments we show that the SSFN can self-estimate its size using the low-complexity algorithm. The size of SSFN varies significantly across the eight datasets.

R3Net: Random Weights, Rectifier Linear Units and Robustness for Artificial Neural Network

We consider a neural network architecture with randomized features, a sign-splitter, followed by rectified linear units (ReLU). We prove that our architecture exhibits robustness to the input perturbation: the output feature of the neural network exhibits a Lipschitz continuity in terms of the input perturbation. We further show that the network output exhibits a discrimination ability that inputs that are not arbitrarily close generate output vectors which maintain distance between each other obeying a certain lower bound. This ensures that two different inputs remain discriminable while contracting the distance in the output feature space.