Neural Greedy Pursuit for Feature Selection
Paper and Code
Jul 19, 2022
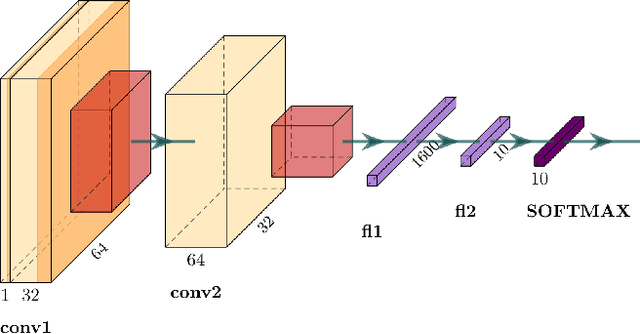


We propose a greedy algorithm to select $N$ important features among $P$ input features for a non-linear prediction problem. The features are selected one by one sequentially, in an iterative loss minimization procedure. We use neural networks as predictors in the algorithm to compute the loss and hence, we refer to our method as neural greedy pursuit (NGP). NGP is efficient in selecting $N$ features when $N \ll P$, and it provides a notion of feature importance in a descending order following the sequential selection procedure. We experimentally show that NGP provides better performance than several feature selection methods such as DeepLIFT and Drop-one-out loss. In addition, we experimentally show a phase transition behavior in which perfect selection of all $N$ features without false positives is possible when the training data size exceeds a threshold.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge