Model Selection in High-Dimensional Block-Sparse Linear Regression

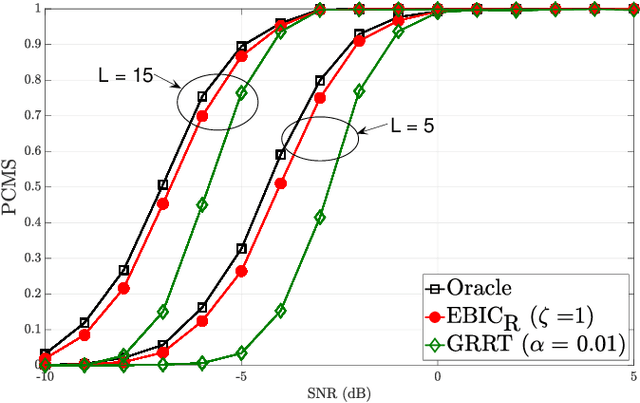
Model selection is an indispensable part of data analysis dealing very frequently with fitting and prediction purposes. In this paper, we tackle the problem of model selection in a general linear regression where the parameter matrix possesses a block-sparse structure, i.e., the non-zero entries occur in clusters or blocks and the number of such non-zero blocks is very small compared to the parameter dimension. Furthermore, a high-dimensional setting is considered where the parameter dimension is quite large compared to the number of available measurements. To perform model selection in this setting, we present an information criterion that is a generalization of the Extended Bayesian Information Criterion-Robust (EBIC-R) and it takes into account both the block structure and the high-dimensionality scenario. The analytical steps for deriving the EBIC-R for this setting are provided. Simulation results show that the proposed method performs considerably better than the existing state-of-the-art methods and achieves empirical consistency at large sample sizes and/or at high-SNR.

Robust Information Criterion for Model Selection in Sparse High-Dimensional Linear Regression Models

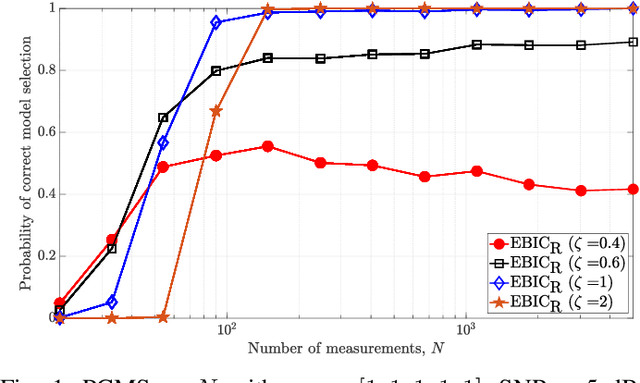
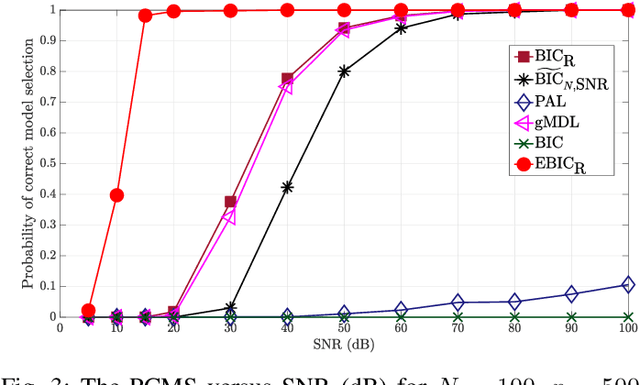
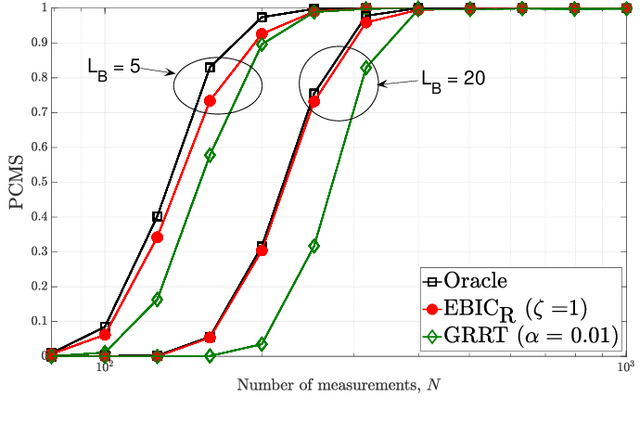
Model selection in linear regression models is a major challenge when dealing with high-dimensional data where the number of available measurements (sample size) is much smaller than the dimension of the parameter space. Traditional methods for model selection such as Akaike information criterion, Bayesian information criterion (BIC) and minimum description length are heavily prone to overfitting in the high-dimensional setting. In this regard, extended BIC (EBIC), which is an extended version of the original BIC and extended Fisher information criterion (EFIC), which is a combination of EBIC and Fisher information criterion, are consistent estimators of the true model as the number of measurements grows very large. However, EBIC is not consistent in high signal-to-noise-ratio (SNR) scenarios where the sample size is fixed and EFIC is not invariant to data scaling resulting in unstable behaviour. In this paper, we propose a new form of the EBIC criterion called EBIC-Robust, which is invariant to data scaling and consistent in both large sample size and high-SNR scenarios. Analytical proofs are presented to guarantee its consistency. Simulation results indicate that the performance of EBIC-Robust is quite superior to that of both EBIC and EFIC.

Statistical model-based evaluation of neural networks

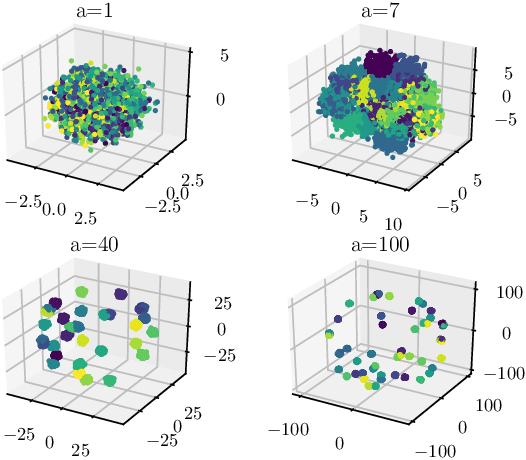
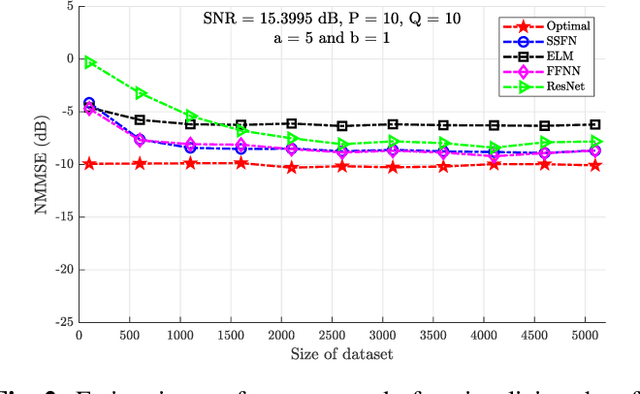
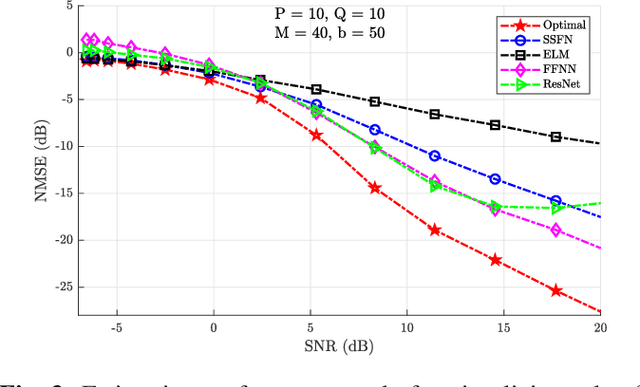
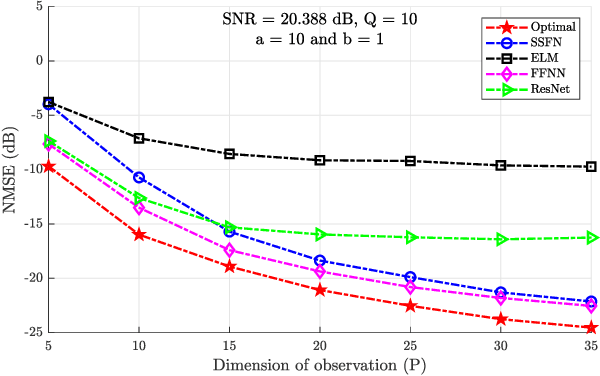
Using a statistical model-based data generation, we develop an experimental setup for the evaluation of neural networks (NNs). The setup helps to benchmark a set of NNs vis-a-vis minimum-mean-square-error (MMSE) performance bounds. This allows us to test the effects of training data size, data dimension, data geometry, noise, and mismatch between training and testing conditions. In the proposed setup, we use a Gaussian mixture distribution to generate data for training and testing a set of competing NNs. Our experiments show the importance of understanding the type and statistical conditions of data for appropriate application and design of NNs