Model Selection in High-Dimensional Block-Sparse Linear Regression

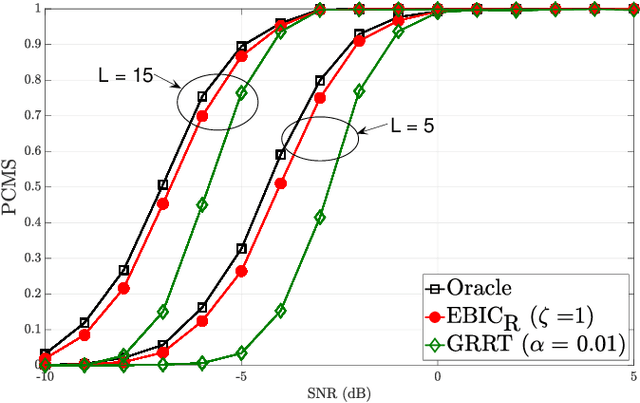
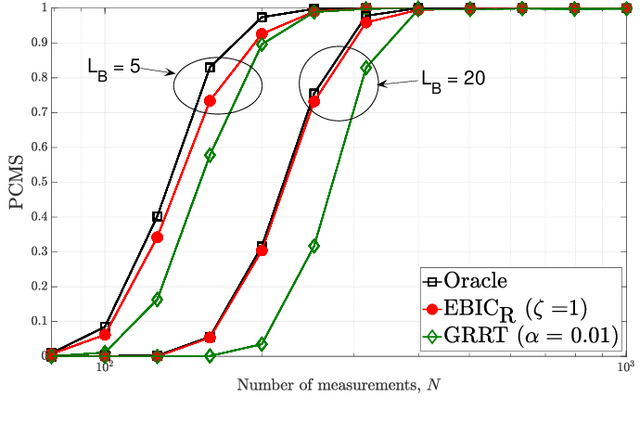
Model selection is an indispensable part of data analysis dealing very frequently with fitting and prediction purposes. In this paper, we tackle the problem of model selection in a general linear regression where the parameter matrix possesses a block-sparse structure, i.e., the non-zero entries occur in clusters or blocks and the number of such non-zero blocks is very small compared to the parameter dimension. Furthermore, a high-dimensional setting is considered where the parameter dimension is quite large compared to the number of available measurements. To perform model selection in this setting, we present an information criterion that is a generalization of the Extended Bayesian Information Criterion-Robust (EBIC-R) and it takes into account both the block structure and the high-dimensionality scenario. The analytical steps for deriving the EBIC-R for this setting are provided. Simulation results show that the proposed method performs considerably better than the existing state-of-the-art methods and achieves empirical consistency at large sample sizes and/or at high-SNR.

Robust Information Criterion for Model Selection in Sparse High-Dimensional Linear Regression Models

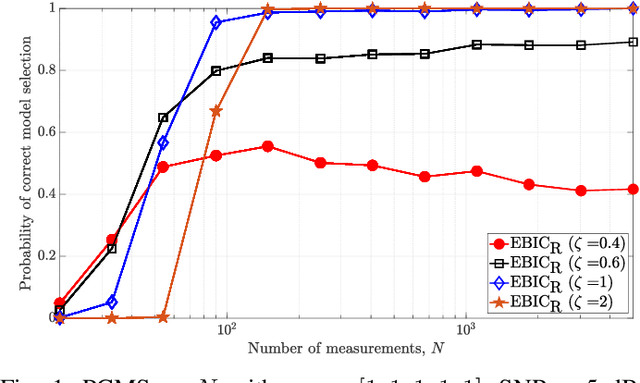
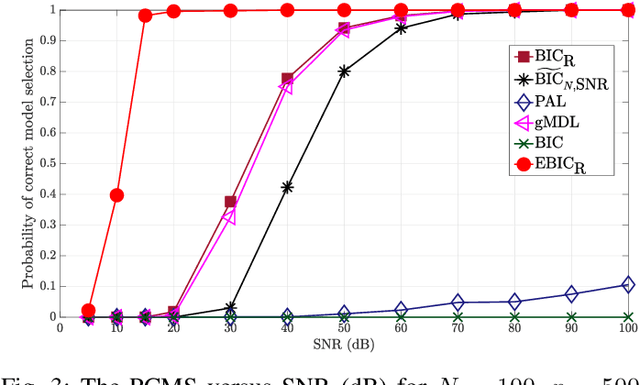
Model selection in linear regression models is a major challenge when dealing with high-dimensional data where the number of available measurements (sample size) is much smaller than the dimension of the parameter space. Traditional methods for model selection such as Akaike information criterion, Bayesian information criterion (BIC) and minimum description length are heavily prone to overfitting in the high-dimensional setting. In this regard, extended BIC (EBIC), which is an extended version of the original BIC and extended Fisher information criterion (EFIC), which is a combination of EBIC and Fisher information criterion, are consistent estimators of the true model as the number of measurements grows very large. However, EBIC is not consistent in high signal-to-noise-ratio (SNR) scenarios where the sample size is fixed and EFIC is not invariant to data scaling resulting in unstable behaviour. In this paper, we propose a new form of the EBIC criterion called EBIC-Robust, which is invariant to data scaling and consistent in both large sample size and high-SNR scenarios. Analytical proofs are presented to guarantee its consistency. Simulation results indicate that the performance of EBIC-Robust is quite superior to that of both EBIC and EFIC.

A Connectedness Constraint for Learning Sparse Graphs

Graphs are naturally sparse objects that are used to study many problems involving networks, for example, distributed learning and graph signal processing. In some cases, the graph is not given, but must be learned from the problem and available data. Often it is desirable to learn sparse graphs. However, making a graph highly sparse can split the graph into several disconnected components, leading to several separate networks. The main difficulty is that connectedness is often treated as a combinatorial property, making it hard to enforce in e.g. convex optimization problems. In this article, we show how connectedness of undirected graphs can be formulated as an analytical property and can be enforced as a convex constraint. We especially show how the constraint relates to the distributed consensus problem and graph Laplacian learning. Using simulated and real data, we perform experiments to learn sparse and connected graphs from data.

Bayesian Learning for Low-Rank matrix reconstruction

We develop latent variable models for Bayesian learning based low-rank matrix completion and reconstruction from linear measurements. For under-determined systems, the developed methods are shown to reconstruct low-rank matrices when neither the rank nor the noise power is known a-priori. We derive relations between the latent variable models and several low-rank promoting penalty functions. The relations justify the use of Kronecker structured covariance matrices in a Gaussian based prior. In the methods, we use evidence approximation and expectation-maximization to learn the model parameters. The performance of the methods is evaluated through extensive numerical simulations.

Combined modeling of sparse and dense noise for improvement of Relevance Vector Machine

Using a Bayesian approach, we consider the problem of recovering sparse signals under additive sparse and dense noise. Typically, sparse noise models outliers, impulse bursts or data loss. To handle sparse noise, existing methods simultaneously estimate the sparse signal of interest and the sparse noise of no interest. For estimating the sparse signal, without the need of estimating the sparse noise, we construct a robust Relevance Vector Machine (RVM). In the RVM, sparse noise and ever present dense noise are treated through a combined noise model. The precision of combined noise is modeled by a diagonal matrix. We show that the new RVM update equations correspond to a non-symmetric sparsity inducing cost function. Further, the combined modeling is found to be computationally more efficient. We also extend the method to block-sparse signals and noise with known and unknown block structures. Through simulations, we show the performance and computation efficiency of the new RVM in several applications: recovery of sparse and block sparse signals, housing price prediction and image denoising.

Relevance Singular Vector Machine for low-rank matrix sensing

In this paper we develop a new Bayesian inference method for low rank matrix reconstruction. We call the new method the Relevance Singular Vector Machine (RSVM) where appropriate priors are defined on the singular vectors of the underlying matrix to promote low rank. To accelerate computations, a numerically efficient approximation is developed. The proposed algorithms are applied to matrix completion and matrix reconstruction problems and their performance is studied numerically.