Robust Information Criterion for Model Selection in Sparse High-Dimensional Linear Regression Models
Paper and Code
Jun 17, 2022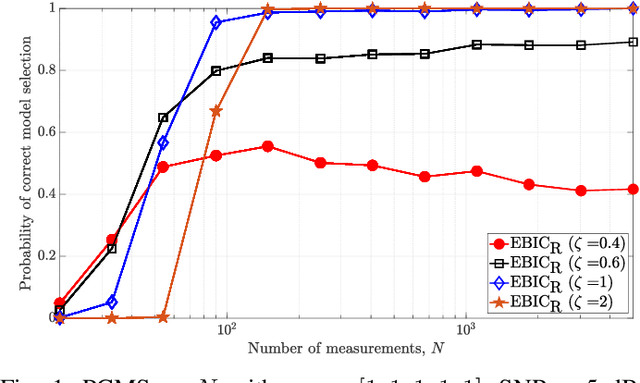

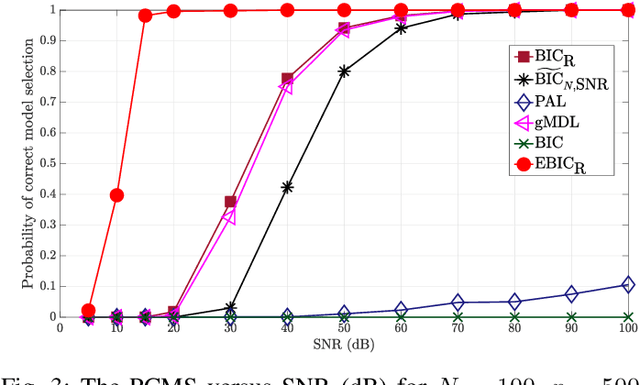

Model selection in linear regression models is a major challenge when dealing with high-dimensional data where the number of available measurements (sample size) is much smaller than the dimension of the parameter space. Traditional methods for model selection such as Akaike information criterion, Bayesian information criterion (BIC) and minimum description length are heavily prone to overfitting in the high-dimensional setting. In this regard, extended BIC (EBIC), which is an extended version of the original BIC and extended Fisher information criterion (EFIC), which is a combination of EBIC and Fisher information criterion, are consistent estimators of the true model as the number of measurements grows very large. However, EBIC is not consistent in high signal-to-noise-ratio (SNR) scenarios where the sample size is fixed and EFIC is not invariant to data scaling resulting in unstable behaviour. In this paper, we propose a new form of the EBIC criterion called EBIC-Robust, which is invariant to data scaling and consistent in both large sample size and high-SNR scenarios. Analytical proofs are presented to guarantee its consistency. Simulation results indicate that the performance of EBIC-Robust is quite superior to that of both EBIC and EFIC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge