Model Selection in High-Dimensional Block-Sparse Linear Regression

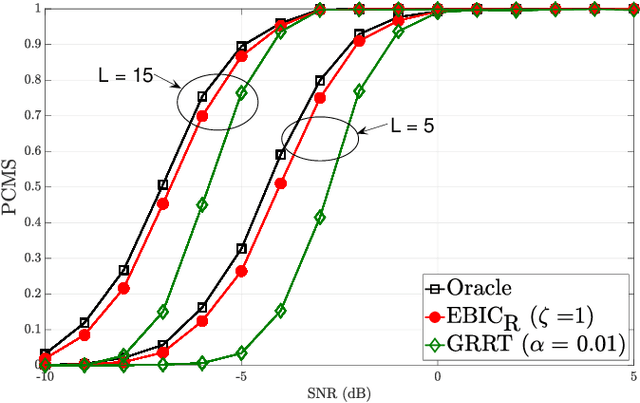
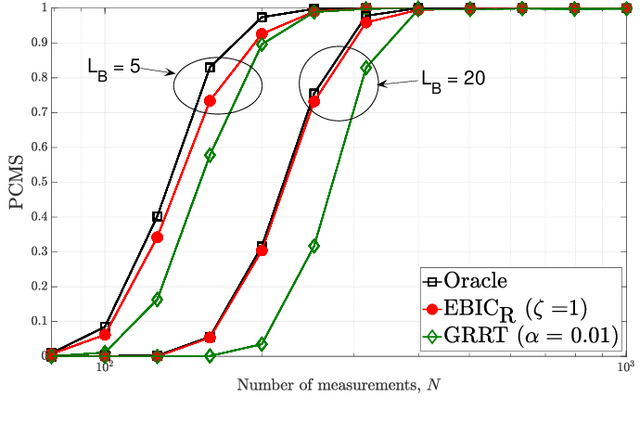
Model selection is an indispensable part of data analysis dealing very frequently with fitting and prediction purposes. In this paper, we tackle the problem of model selection in a general linear regression where the parameter matrix possesses a block-sparse structure, i.e., the non-zero entries occur in clusters or blocks and the number of such non-zero blocks is very small compared to the parameter dimension. Furthermore, a high-dimensional setting is considered where the parameter dimension is quite large compared to the number of available measurements. To perform model selection in this setting, we present an information criterion that is a generalization of the Extended Bayesian Information Criterion-Robust (EBIC-R) and it takes into account both the block structure and the high-dimensionality scenario. The analytical steps for deriving the EBIC-R for this setting are provided. Simulation results show that the proposed method performs considerably better than the existing state-of-the-art methods and achieves empirical consistency at large sample sizes and/or at high-SNR.