SSFN: Self Size-estimating Feed-forward Network and Low Complexity Design

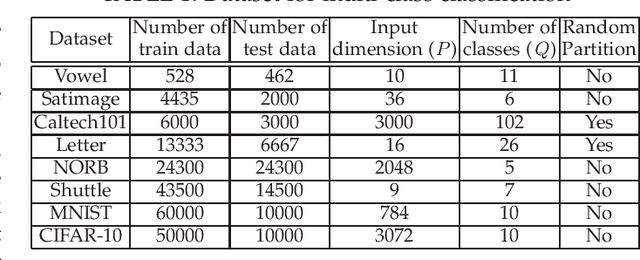
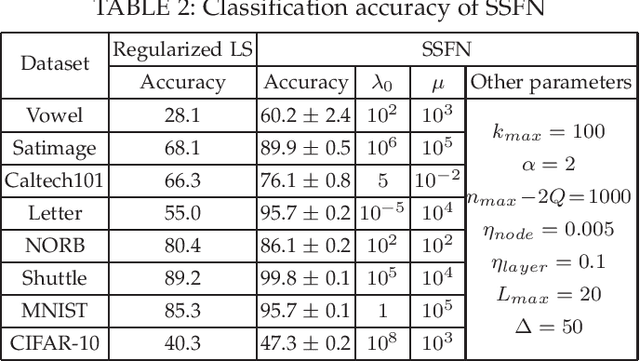
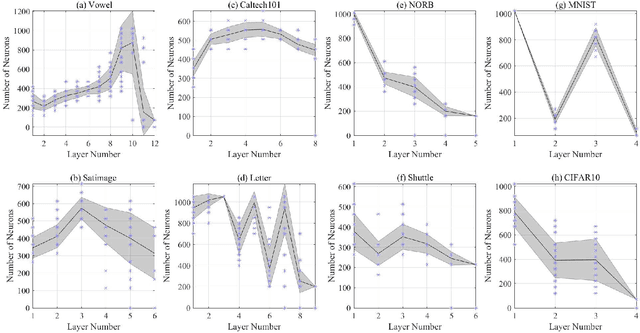
We design a self size-estimating feed-forward network (SSFN) using a joint optimization approach for estimation of number of layers, number of nodes and learning of weight matrices at a low computational complexity. In the proposed approach, SSFN grows from a small-size network to a large-size network. The increase in size from small-size to large-size guarantees a monotonically decreasing cost with addition of nodes and layers. The optimization approach uses a sequence of layer-wise target-seeking non-convex optimization problems. Using `lossless flow property' of some activation functions, such as rectified linear unit (ReLU), we analytically find regularization parameters in the layer-wise non-convex optimization problems. Closed-form analytic expressions of regularization parameters allow to avoid tedious cross-validations. The layer-wise non-convex optimization problems are further relaxed to convex optimization problems for ease of implementation and analytical tractability. The convex relaxation helps to design a low-complexity algorithm for construction of the SSFN. We experiment with eight popular benchmark datasets for sound and image classification tasks. Using extensive experiments we show that the SSFN can self-estimate its size using the low-complexity algorithm. The size of SSFN varies significantly across the eight datasets.