Progressive Learning for Systematic Design of Large Neural Networks
Paper and Code
Oct 23, 2017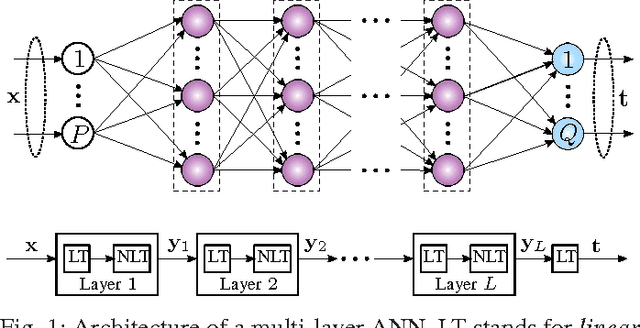
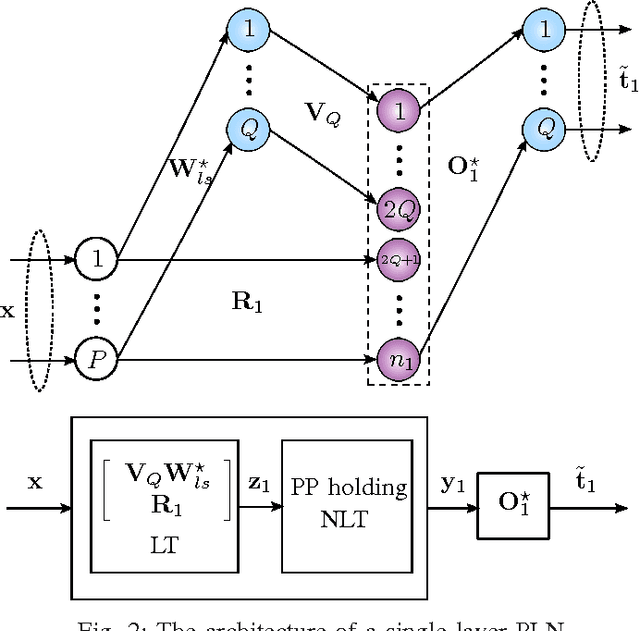
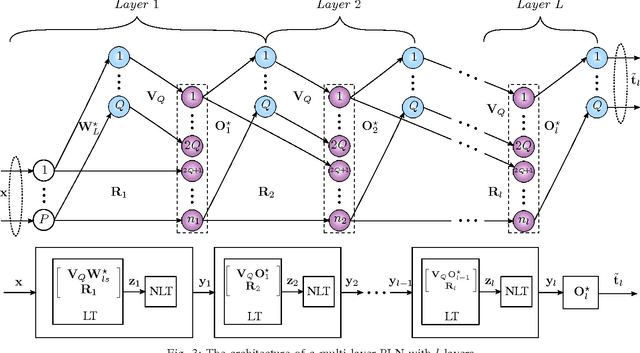
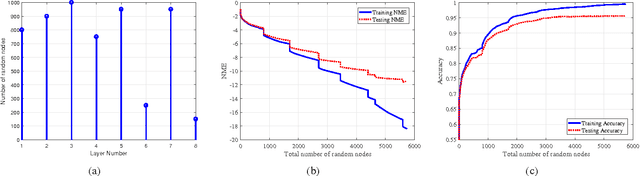
We develop an algorithm for systematic design of a large artificial neural network using a progression property. We find that some non-linear functions, such as the rectifier linear unit and its derivatives, hold the property. The systematic design addresses the choice of network size and regularization of parameters. The number of nodes and layers in network increases in progression with the objective of consistently reducing an appropriate cost. Each layer is optimized at a time, where appropriate parameters are learned using convex optimization. Regularization parameters for convex optimization do not need a significant manual effort for tuning. We also use random instances for some weight matrices, and that helps to reduce the number of parameters we learn. The developed network is expected to show good generalization power due to appropriate regularization and use of random weights in the layers. This expectation is verified by extensive experiments for classification and regression problems, using standard databases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge