Locally Convex Sparse Learning over Networks
Paper and Code
Mar 31, 2018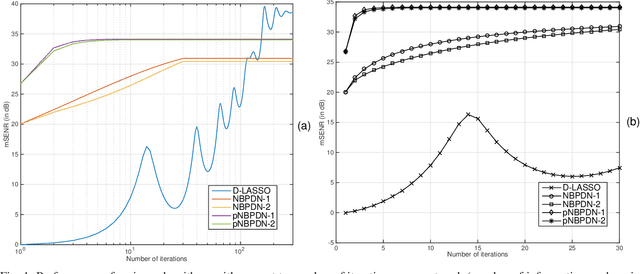


We consider a distributed learning setup where a sparse signal is estimated over a network. Our main interest is to save communication resource for information exchange over the network and reduce processing time. Each node of the network uses a convex optimization based algorithm that provides a locally optimum solution for that node. The nodes exchange their signal estimates over the network in order to refine their local estimates. At a node, the optimization algorithm is based on an $\ell_1$-norm minimization with appropriate modifications to promote sparsity as well as to include influence of estimates from neighboring nodes. Our expectation is that local estimates in each node improve fast and converge, resulting in a limited demand for communication of estimates between nodes and reducing the processing time. We provide restricted-isometry-property (RIP)-based theoretical analysis on estimation quality. In the scenario of clean observation, it is shown that the local estimates converge to the exact sparse signal under certain technical conditions. Simulation results show that the proposed algorithms show competitive performance compared to a globally optimum distributed LASSO algorithm in the sense of convergence speed and estimation error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge