Translation Insensitive CNNs

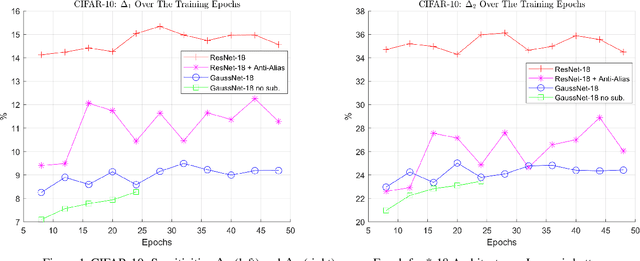
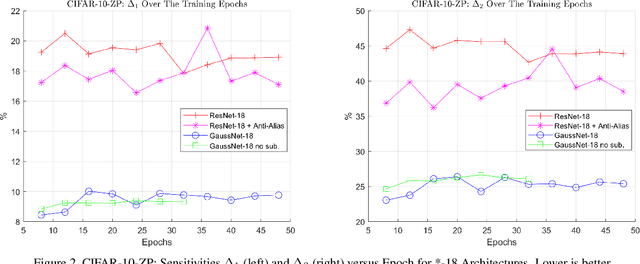
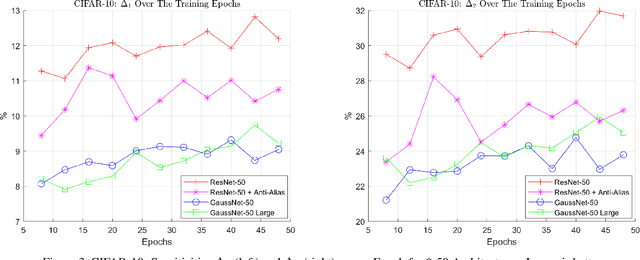
We address the problem that state-of-the-art Convolution Neural Networks (CNN) classifiers are not invariant to small shifts. The problem can be solved by the removal of sub-sampling operations such as stride and max pooling, but at a cost of severely degraded training and test efficiency. We present a novel usage of Gaussian-Hermite basis to efficiently approximate arbitrary filters within the CNN framework to obtain translation invariance. This is shown to be invariant to small shifts, and preserves the efficiency of training. Further, to improve efficiency in memory usage as well as computational speed, we show that it is still possible to sub-sample with this approach and retain a weaker form of invariance that we call \emph{translation insensitivity}, which leads to stability with respect to shifts. We prove these claims analytically and empirically. Our analytic methods further provide a framework for understanding any architecture in terms of translation insensitivity, and provide guiding principles for design.

Towards Robust Deep Neural Networks

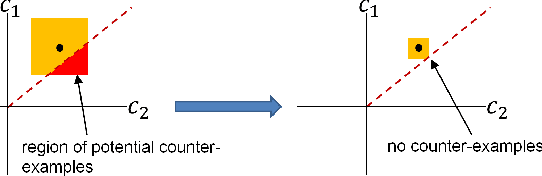
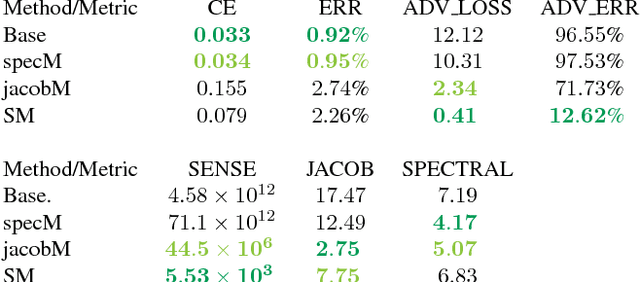
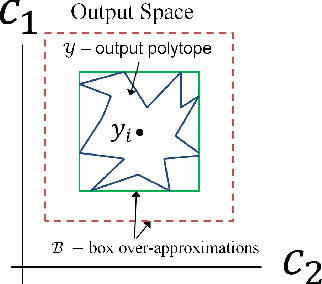
We examine the relationship between the energy landscape of neural networks and their robustness to adversarial attacks. Combining energy landscape techniques developed in computational chemistry with tools drawn from formal methods, we produce empirical evidence that networks corresponding to lower-lying minima in the landscape tend to be more robust. The robustness measure used is the inverse of the sensitivity measure, which we define as the volume of an over-approximation of the reachable set of network outputs under all additive $l_{\infty}$ bounded perturbations on the input data. We present a novel loss function which contains a weighted sensitivity component in addition to the traditional task-oriented and regularization terms. In our experiments on standard machine learning and computer vision datasets (e.g., Iris and MNIST), we show that the proposed loss function leads to networks which reliably optimize the robustness measure as well as other related metrics of adversarial robustness without significant degradation in the classification error.