HAct: Out-of-Distribution Detection with Neural Net Activation Histograms

We propose a simple, efficient, and accurate method for detecting out-of-distribution (OOD) data for trained neural networks, a potential first step in methods for OOD generalization. We propose a novel descriptor, HAct - activation histograms, for OOD detection, that is, probability distributions (approximated by histograms) of output values of neural network layers under the influence of incoming data. We demonstrate that HAct is significantly more accurate than state-of-the-art on multiple OOD image classification benchmarks. For instance, our approach achieves a true positive rate (TPR) of 95% with only 0.05% false-positives using Resnet-50 on standard OOD benchmarks, outperforming previous state-of-the-art by 20.66% in the false positive rate (at the same TPR of 95%). The low computational complexity and the ease of implementation make HAct suitable for online implementation in monitoring deployed neural networks in practice at scale.

StEik: Stabilizing the Optimization of Neural Signed Distance Functions and Finer Shape Representation

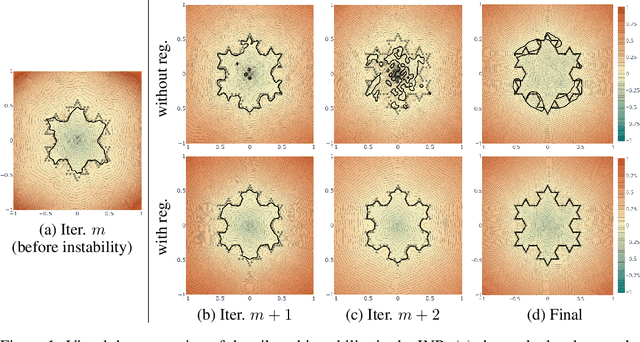
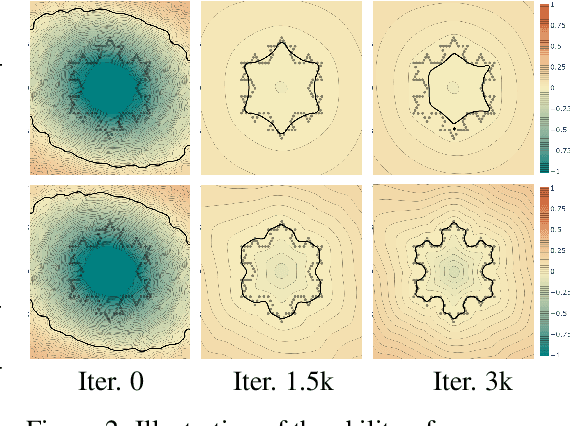
We present new insights and a novel paradigm (StEik) for learning implicit neural representations (INR) of shapes. In particular, we shed light on the popular eikonal loss used for imposing a signed distance function constraint in INR. We show analytically that as the representation power of the network increases, the optimization approaches a partial differential equation (PDE) in the continuum limit that is unstable. We show that this instability can manifest in existing network optimization, leading to irregularities in the reconstructed surface and/or convergence to sub-optimal local minima, and thus fails to capture fine geometric and topological structure. We show analytically how other terms added to the loss, currently used in the literature for other purposes, can actually eliminate these instabilities. However, such terms can over-regularize the surface, preventing the representation of fine shape detail. Based on a similar PDE theory for the continuum limit, we introduce a new regularization term that still counteracts the eikonal instability but without over-regularizing. Furthermore, since stability is now guaranteed in the continuum limit, this stabilization also allows for considering new network structures that are able to represent finer shape detail. We introduce such a structure based on quadratic layers. Experiments on multiple benchmark data sets show that our new regularization and network are able to capture more precise shape details and more accurate topology than existing state-of-the-art.

Flow-Guided Video Inpainting with Scene Templates

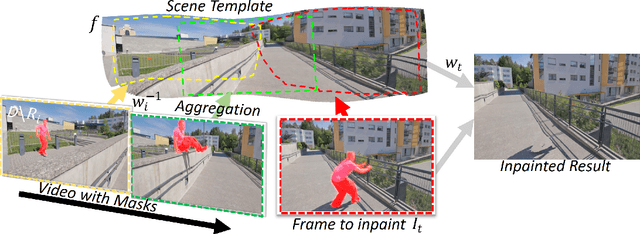
We consider the problem of filling in missing spatio-temporal regions of a video. We provide a novel flow-based solution by introducing a generative model of images in relation to the scene (without missing regions) and mappings from the scene to images. We use the model to jointly infer the scene template, a 2D representation of the scene, and the mappings. This ensures consistency of the frame-to-frame flows generated to the underlying scene, reducing geometric distortions in flow based inpainting. The template is mapped to the missing regions in the video by a new L2-L1 interpolation scheme, creating crisp inpaintings and reducing common blur and distortion artifacts. We show on two benchmark datasets that our approach out-performs state-of-the-art quantitatively and in user studies.

Class-Agnostic Segmentation Loss and Its Application to Salient Object Detection and Segmentation

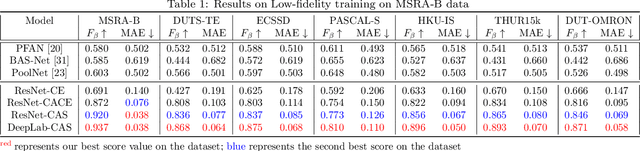
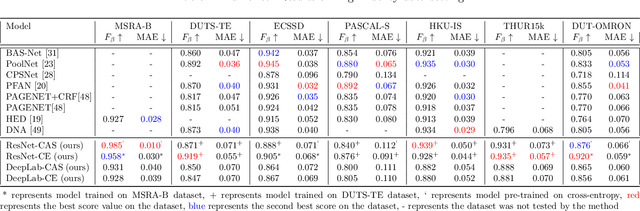
In this paper we present a novel loss function, called class-agnostic segmentation (CAS) loss. With CAS loss the class descriptors are learned during training of the network. We don't require to define the label of a class a-priori, rather the CAS loss clusters regions with similar appearance together in a weakly-supervised manner. Furthermore, we show that the CAS loss function is sparse, bounded, and robust to class-imbalance. We first apply our CAS loss function with fully-convolutional ResNet101 and DeepLab-v3 architectures to the binary segmentation problem of salient object detection. We investigate the performance against the state-of-the-art methods in two settings of low and high-fidelity training data on seven salient object detection datasets. For low-fidelity training data (incorrect class label) class-agnostic segmentation loss outperforms the state-of-the-art methods on salient object detection datasets by staggering margins of around 50%. For high-fidelity training data (correct class labels) class-agnostic segmentation models perform as good as the state-of-the-art approaches while beating the state-of-the-art methods on most datasets. In order to show the utility of the loss function across different domains we then also test on general segmentation dataset, where class-agnostic segmentation loss outperforms competing losses by huge margins.

Shape-Tailored Deep Neural Networks

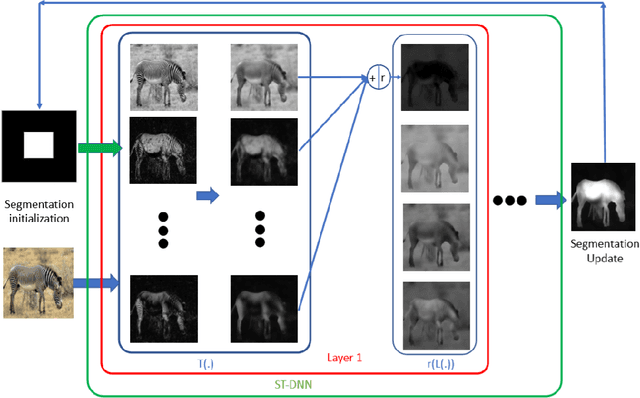
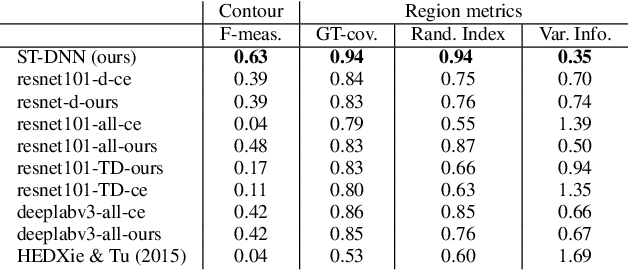
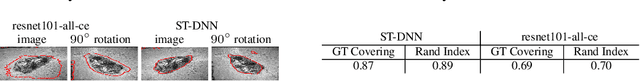
We present Shape-Tailored Deep Neural Networks (ST-DNN). ST-DNN extend convolutional networks (CNN), which aggregate data from fixed shape (square) neighborhoods, to compute descriptors defined on arbitrarily shaped regions. This is natural for segmentation, where descriptors should describe regions (e.g., of objects) that have diverse shape. We formulate these descriptors through the Poisson partial differential equation (PDE), which can be used to generalize convolution to arbitrary regions. We stack multiple PDE layers to generalize a deep CNN to arbitrary regions, and apply it to segmentation. We show that ST-DNN are covariant to translations and rotations and robust to domain deformations, natural for segmentation, which existing CNN based methods lack. ST-DNN are 3-4 orders of magnitude smaller then CNNs used for segmentation. We show that they exceed segmentation performance compared to state-of-the-art CNN-based descriptors using 2-3 orders smaller training sets on the texture segmentation problem.

Channel-Directed Gradients for Optimization of Convolutional Neural Networks

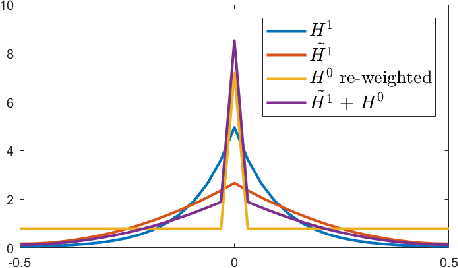
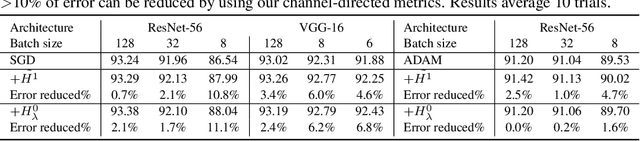
We introduce optimization methods for convolutional neural networks that can be used to improve existing gradient-based optimization in terms of generalization error. The method requires only simple processing of existing stochastic gradients, can be used in conjunction with any optimizer, and has only a linear overhead (in the number of parameters) compared to computation of the stochastic gradient. The method works by computing the gradient of the loss function with respect to output-channel directed re-weighted L2 or Sobolev metrics, which has the effect of smoothing components of the gradient across a certain direction of the parameter tensor. We show that defining the gradients along the output channel direction leads to a performance boost, while other directions can be detrimental. We present the continuum theory of such gradients, its discretization, and application to deep networks. Experiments on benchmark datasets, several networks and baseline optimizers show that optimizers can be improved in generalization error by simply computing the stochastic gradient with respect to output-channel directed metrics.

Phase Consistent Ecological Domain Adaptation

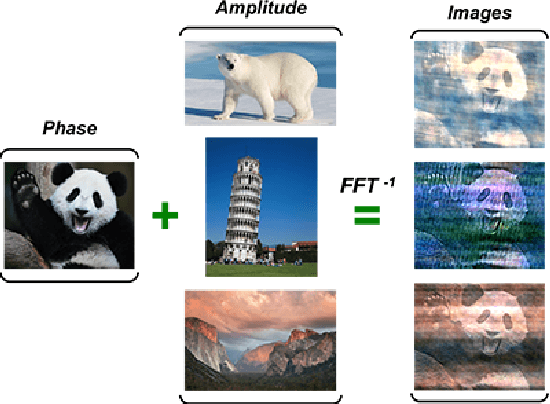
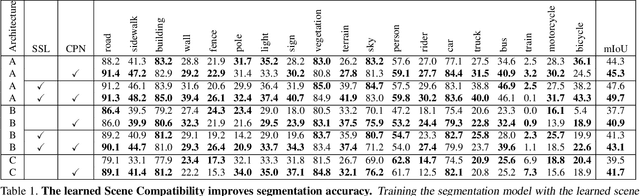
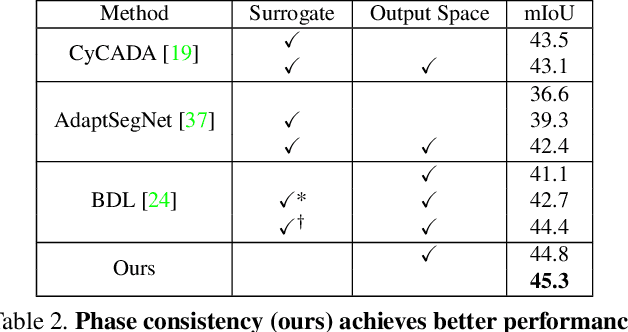
We introduce two criteria to regularize the optimization involved in learning a classifier in a domain where no annotated data are available, leveraging annotated data in a different domain, a problem known as unsupervised domain adaptation. We focus on the task of semantic segmentation, where annotated synthetic data are aplenty, but annotating real data is laborious. The first criterion, inspired by visual psychophysics, is that the map between the two image domains be phase-preserving. This restricts the set of possible learned maps, while enabling enough flexibility to transfer semantic information. The second criterion aims to leverage ecological statistics, or regularities in the scene which are manifest in any image of it, regardless of the characteristics of the illuminant or the imaging sensor. It is implemented using a deep neural network that scores the likelihood of each possible segmentation given a single un-annotated image. Incorporating these two priors in a standard domain adaptation framework improves performance across the board in the most common unsupervised domain adaptation benchmarks for semantic segmentation.

Translation Insensitive CNNs

We address the problem that state-of-the-art Convolution Neural Networks (CNN) classifiers are not invariant to small shifts. The problem can be solved by the removal of sub-sampling operations such as stride and max pooling, but at a cost of severely degraded training and test efficiency. We present a novel usage of Gaussian-Hermite basis to efficiently approximate arbitrary filters within the CNN framework to obtain translation invariance. This is shown to be invariant to small shifts, and preserves the efficiency of training. Further, to improve efficiency in memory usage as well as computational speed, we show that it is still possible to sub-sample with this approach and retain a weaker form of invariance that we call \emph{translation insensitivity}, which leads to stability with respect to shifts. We prove these claims analytically and empirically. Our analytic methods further provide a framework for understanding any architecture in terms of translation insensitivity, and provide guiding principles for design.

Minimum Delay Object Detection From Video

We consider the problem of detecting objects, as they come into view, from videos in an online fashion. We provide the first real-time solution that is guaranteed to minimize the delay, i.e., the time between when the object comes in view and the declared detection time, subject to acceptable levels of detection accuracy. The method leverages modern CNN-based object detectors that operate on a single frame, to aggregate detection results over frames to provide reliable detection at a rate, specified by the user, in guaranteed minimal delay. To do this, we formulate the problem as a Quickest Detection problem, which provides the aforementioned guarantees. We derive our algorithms from this theory. We show in experiments, that with an overhead of just 50 fps, we can increase the number of correct detections and decrease the overall computational cost compared to running a modern single-frame detector.